Lecture 3-4 Soft Shadow

Recap of Shadow Mapping - 点光源

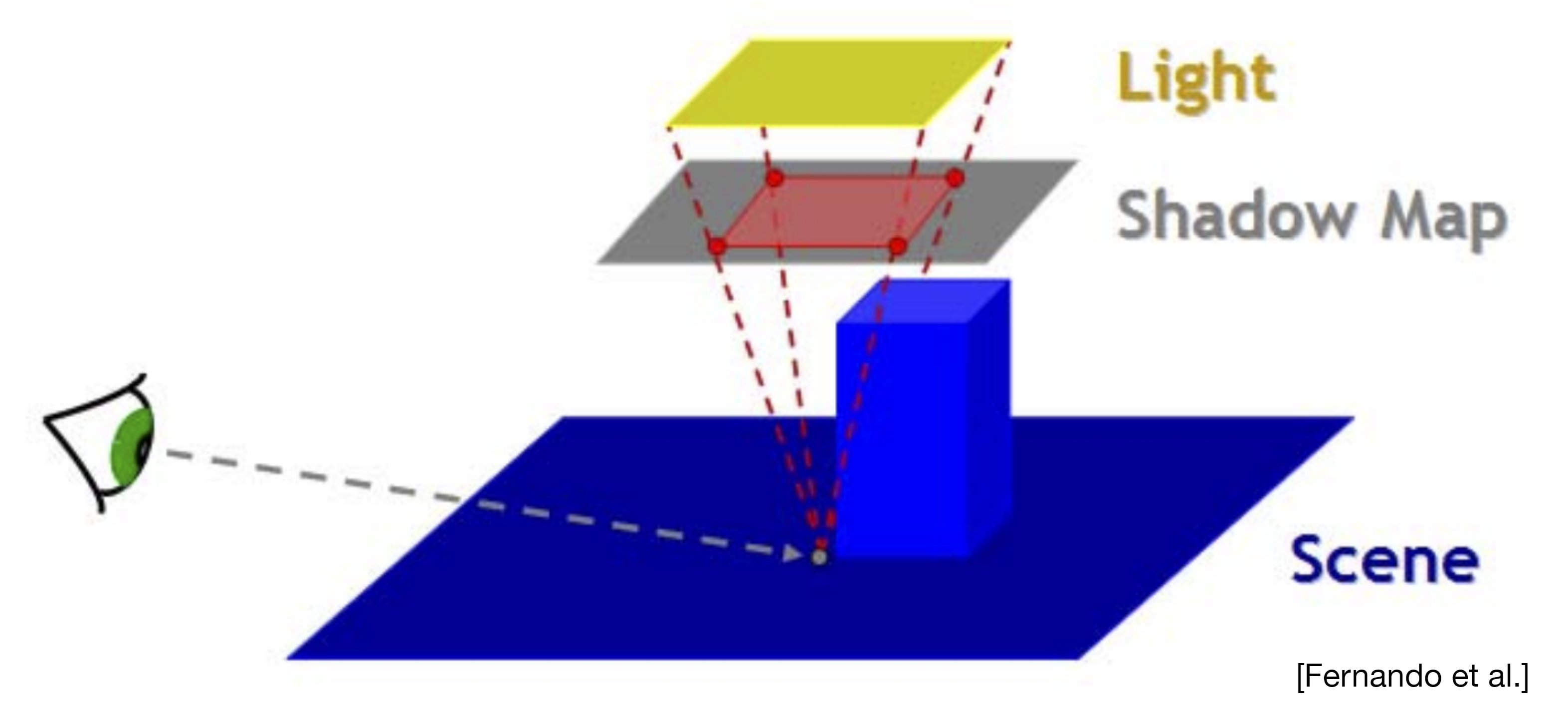
  1. 从“Light”处看向场景，生成场景关于光源的深度图，即Shadow Map；
  2. 从相机处看向场景渲染画面，利用Shadow Map判断像素是否在阴影中。

Feature：

  • 基于二维图像的算法，而不需要三维几何场景
  • 使用透视投影后Z值或透视投影前实际距离生成深度图皆可，Shadow Map与阴影生成时的深度判定方式一致即可

Problem

  • Self occlusion 自遮挡

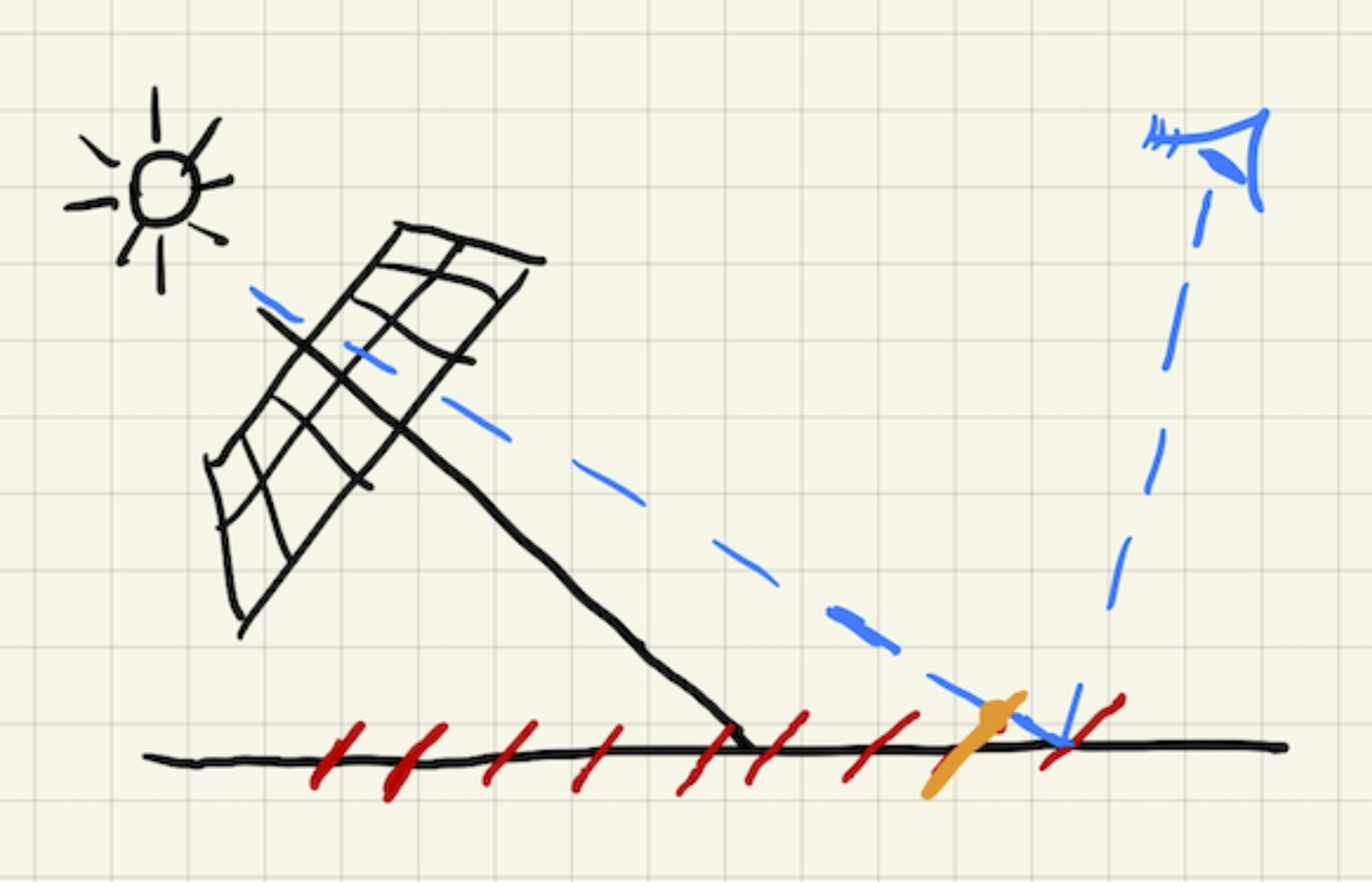
    Shadow Map的每一个像素记录同一深度，形成下图现象。在单个/行像素采样处，形成尺寸为像素宽高的遮挡面。 SelfOcclusion1

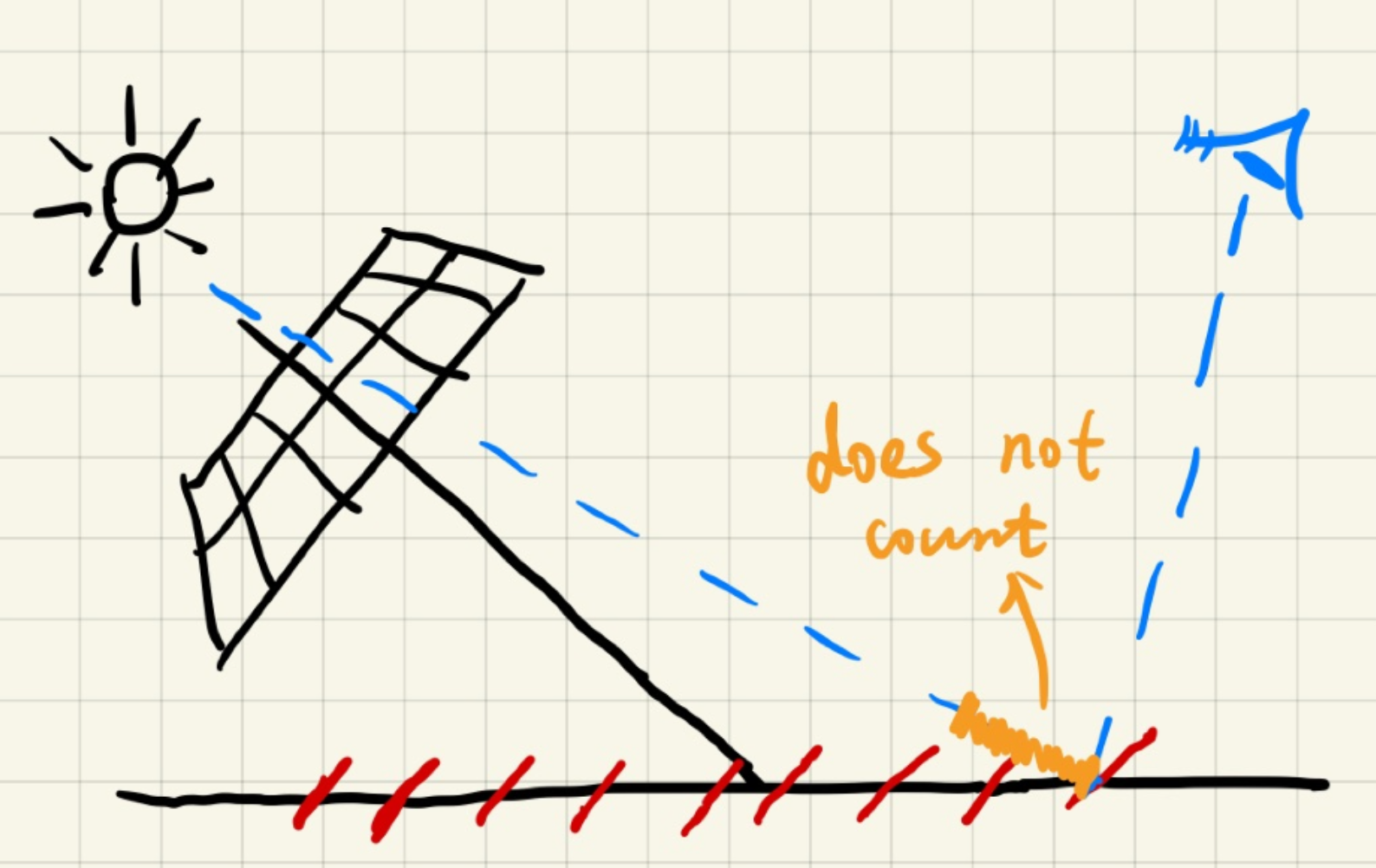
    解决方案：在反射表面邻近区域不计算遮挡。不计算区域Light长度（Bias）由Light与反射表面法线夹角决定。（Light垂直于表面时不产生自遮挡问题）。——带来新问题：丢失遮挡关系。SelfOcclusion2

  • Detached shadow 由解决自遮挡的Bias不计算带来的阴影残缺问题。

    工业界无法彻底解决该问题，通过找到合适的Bias值减少视觉问题。

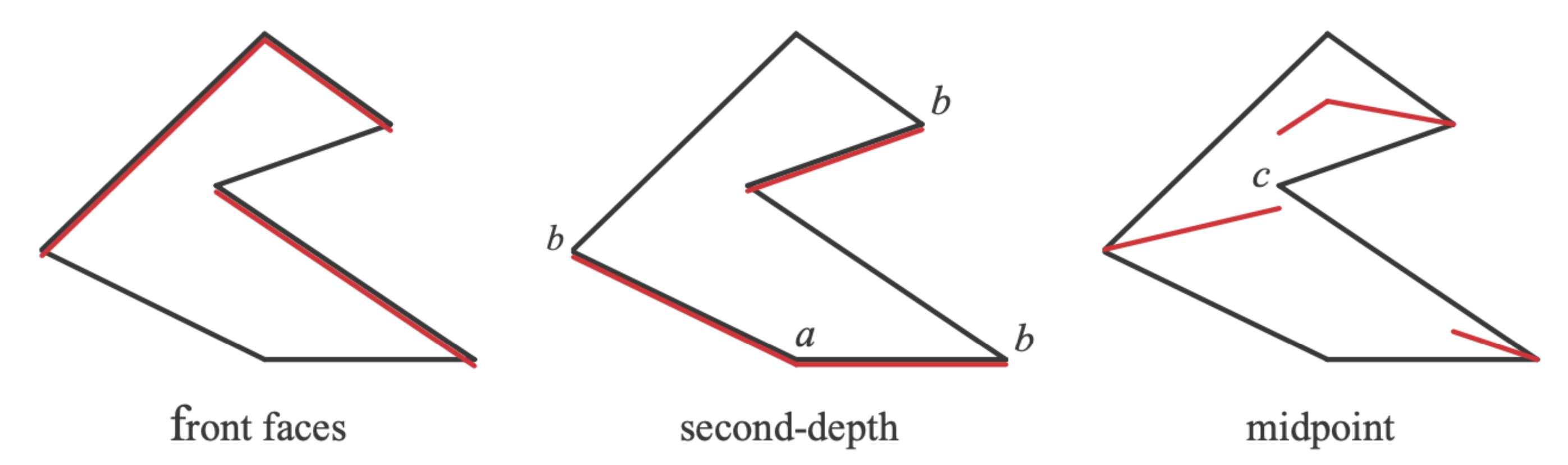
    学术解决方案：Second-depth shadow mapping

    • 存储第一深度和次级深度（离得第二近的表面距离），取中间值作为深度判断的值。
    • 存在问题：要求所有物体watertight（有正反面）；计算量过大。
    • 实时渲染不相信复杂度，只相信绝对速度！因此工业界不适用。

    SecondDepthSM

  • Aliasing 采样

The math behind shadow mapping

微积分中常见的不等式： \[ \begin{array}{c} Schwarz不等式： \displaystyle\left[\int_a^bf(x)g(x)\,\mathrm d x\right]^2\le\int_a^bf^2(x)\,\mathrm d x\cdot\int_a^bg^2(x)\,\mathrm d x\\ Minkowski不等式：\displaystyle\left\{\int_a^b\left[f(x)+g(x)\right]^2\,\mathrm d x\right\}^\frac{1}{2}\le\left\{\int_a^bf^2(x)\,\mathrm d x\right\}^\frac{1}{2}+\left\{\int_a^bg^2(x)\,\mathrm d x\right\}^\frac{1}{2} \end{array} \] Approximation in RTR: But we care more about “approximately equal”. 实时渲染中常将不等式当作约等式使用。

An important approximation: \[ \displaystyle\int_\Omega f(x)g(x)\,\mathrm d x\approx\frac{\int_\Omega f(x)\,\mathrm d x}{\int_\Omega \,\mathrm d x}\cdot\int_\Omega g(x)\,\mathrm d x \]

其中 \(\int_\Omega \,\mathrm d x\) 为归一化常数。

该式何时较准确：

  • 积分域较小时
  • \(g(x)\) 在积分域内变化不大（Smooth）

Recall：Rendering Equation with Explicit Visibility \[ L_o(p,\omega_o)=\int_{\Omega+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)\cos\theta_iV(p,\omega_i)\,\mathrm d \omega_i \] Approximated as: \[ L_o(p,\omega_o)\approx\frac{\int_{\Omega+}V(p,\omega_i)d\omega_i}{\int_{\Omega+}d\omega_i}\cdot\int_{\Omega+}L_i(p,L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)\cos\theta_i\,\mathrm d \omega_i \] 即将Visibility部分 \(V(p,\omega_i)\) 单独计算。则非Visibility部分为纯Shading部分，Visibility近似部分为“Shadow Mapping”部分。

何时准确：

  • 点光源/方向光源（积分域小）
  • Diffuse/面光源（其中一个积分函数平滑）

Ambient Occlusion 环境光遮蔽中将再次用到类似的约等式

PCSS: Percentage Closer Soft Shadows

PCF: Percentage Closer Filtering
  • [ For anti-aliasing at shadows’ edges - Not for soft shadows ]
  • Filtering the result of shadow comparisons

[Solution]

  • 根据Shadow Map判断像素是否在阴影中：不判断一个像素，判断对应像素周围的一圈像素（如7*7网格）
  • 得到该组像素判断的平均值，赋给中心像素（原判断像素）
  • 计算量？PCSS时一并解决
  • 将Filter范围再放大得到软阴影？！
PCSS

  • 软阴影：近处锐利，远处模糊 —— Filter Size <-> Blocker Distance

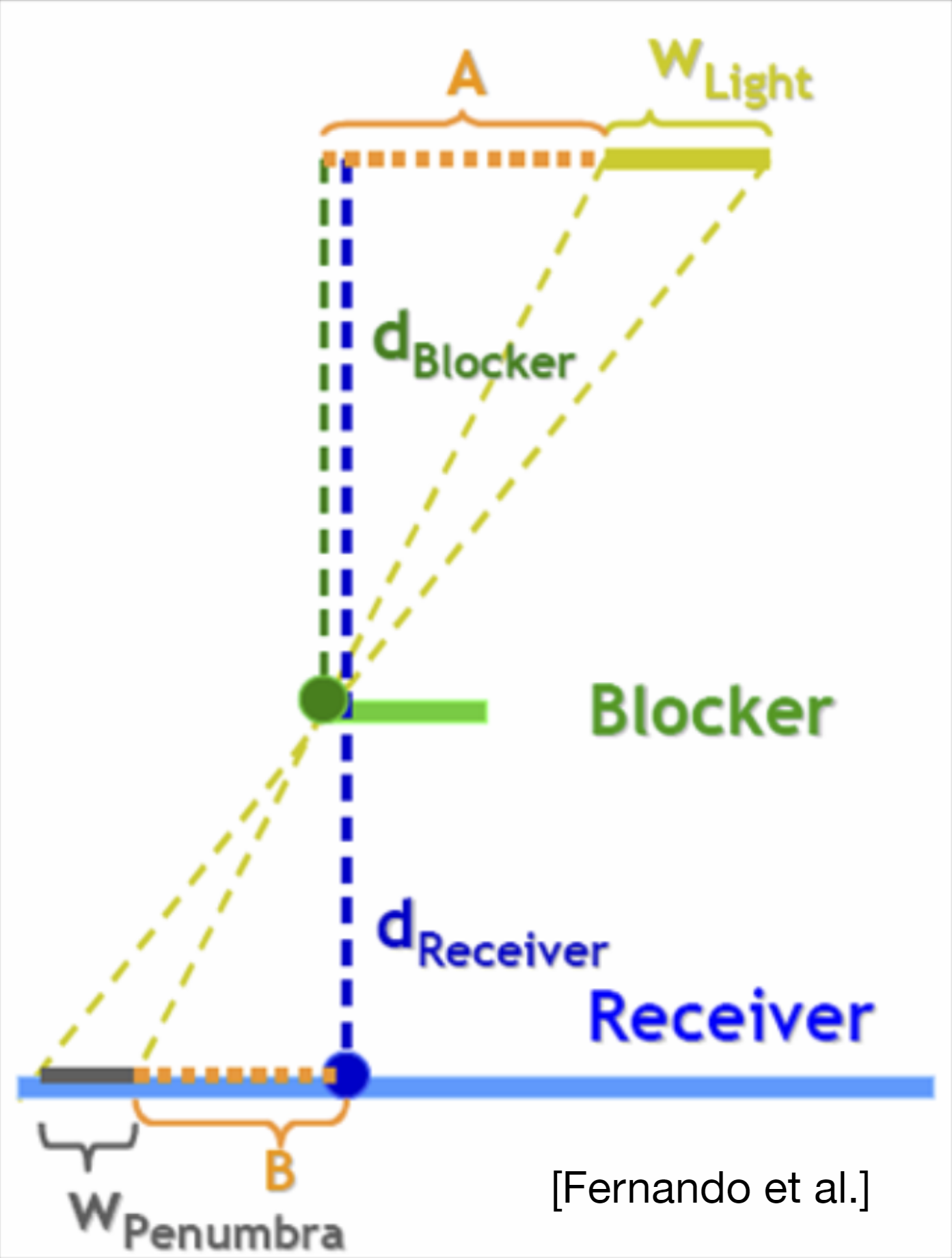
  • \(w_{Penumbra}=(d_{recevier}-d_{Blocker})\cdot w_{Light}/d_{Blocker}\) PCSS1

  • Block Depth: Average block depth 在一定范围内，一个Shading Point被遮挡的平均深度值

  • Complete algorithm

    1. Blocker search : Getting the average depth in a certain region （视面光源中心为点光源生成Shadow Map）
    2. Penumbra estimation : Use the average blocker depth to determine filter size
    3. Percentage Closer Filtering

  • Blocker search的范围（得到Average block depth的方式）如何确定？

    • 取固定范围，如5*5

    • [Better] 取决于光源面积和光照接收面到光源的距离 PCSS2 \[ \rm size_{Blocker}=distance_{ShadowMap2Scene}/distance_{Light2Scene}\cdot size_{Light} \]

  • 开销巨大：下节课解决

A deeper look at PCF

The math behind PCF: Filter/Convolution \[ [w*f](p)=\sum_{q\in\mathcal{N}(p)}w(p,q)f(q)\quad\quad N(p):p的邻域 \] In PCSS \[ V(x)=\sum_{q\in\mathcal{N}(p)}w(p,q)\cdot\chi^+[D_{SM}(q)-D_{scene}(x)]\quad\quad\chi^+(A)=A>0?1:0 \] 因此：

  • PCF并不是对Shadow Map的滤波 \[ V(x)\neq\chi^+\{[w*D_{SM}](q)-D_{scene}(x)\} \]
  • PCF也不是对结果图像做滤波 \[ V(x)\neq\sum_{q\in\mathcal{N}(p)}w(p,q)V(q) \]
More about PCSS

[Blocker Search] and [PCF] is slow to look at every texel.

  • [Blocker Search] 随机取样 => Noise
  • [PCF] Filter范围过大，随机采样 -> 图像空间降噪

Variance Soft Shadow Mapping

  • Fast blocker search and filtering

[ Filter ] PCF：根据正态分布可估计 Percentage Closer Value 正态分布由均值mean和方差variance定义

  • Mean
    • Hardware Mipmaping 但只能正方形
    • Summed Area Tables (SAT)
  • Variance
    • \[ Var(X)=E(X^2)-E^2(X)\quad E:期望=均值 \]
    • 另一张“Shadow Map”记录深度的平方，称为“Square depth map”

由此得到正态分布图，求得CDF(x) of the Gaussian PDF即可（即0-x的积分）。 该积分没有解析解只有数值解，可通过高斯分布积分表Error Function得到CDF值。在cpp中使用erf()求数值解，但计算仍较复杂。

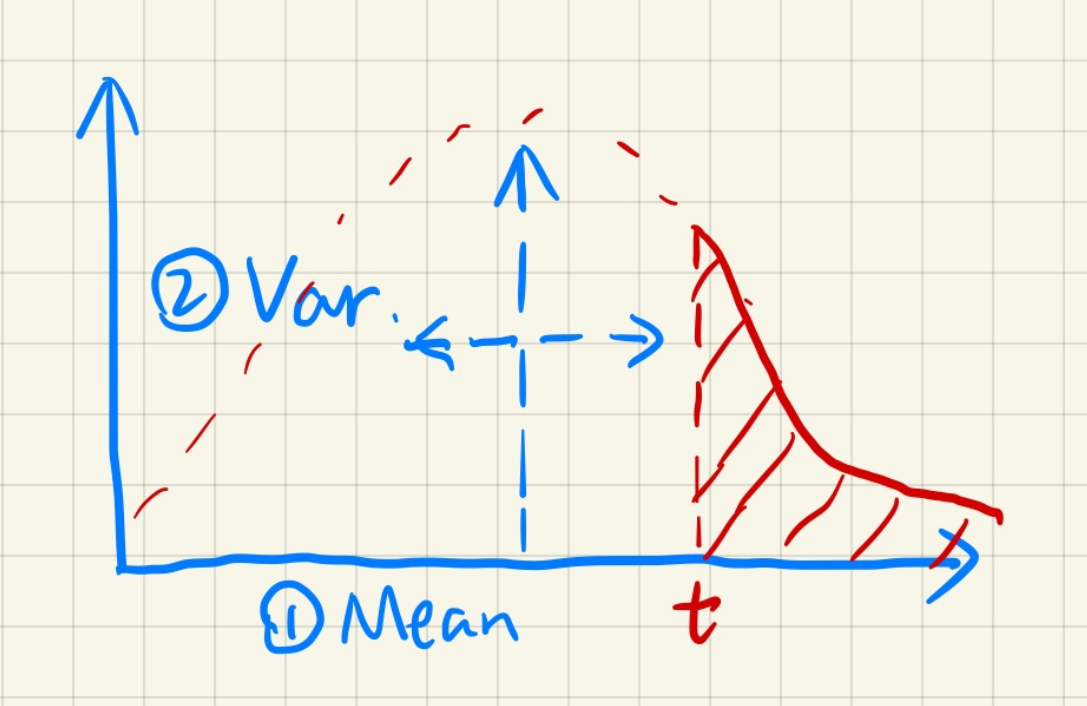
因此引入切比雪夫不等式估计值： \[ P(x>t)\le\frac{\sigma^2}{\sigma^2+(t-\mu)^2}\quad\quad\begin{aligned}\mu&: mean\\\sigma^2&:variance\end{aligned} \] 对任意分布方式，通过切比雪夫不等式估得右侧积分值 \(P(x>t)\) ，再由 \(1-P(x>t)\) 得到 \(CDF(x)\) 。 仅t>mean时较准，但工业界往往直接用。

VSSM1

总结 + Shadow map generation + “Square depth map” + Runtime + Mean of depth in a range: O(1) + Mean of depth square in a range: O(1) + Chebychev: O(1) + No samples / loops needed + Perfectly ? 改变视角需要重新生成map 产生较大开销 GPU解决起来速度非常快

[ Block Search ]

  • Target: The average depth of blockers ( texels whose depth z < t, \(z_{occ}\) ) \(\Rightarrow\begin{array}{l}blocker:z_{occ}\\non-blocker:z_{unocc}\end{array}\)

  • \[ \displaystyle\frac{N_1}{N}z_{unocc}+\frac{N_2}{N}z_{occ}=z_{avg} \]

  • Chebychev Approximation: \(\displaystyle\frac{N_1}{N}=P(x>t)\quad\frac{N_2}{N}=1-P(x>t)\)

  • Approximation: \(z_{unocc}=t\)

MIPMAP and Summed-Area Variance Shadow Maps

Recall: MIPMAP
  • fast, approx., square range queries
  • 非 \(1/n^i\) 方形区域，需使用线性插值
  • 不精准，限制多
SAT (Summed-Area Table)

  • in 1D: 第 \(i\) 位存储 \(0-i\) 的和

    SAT[0] = Arr[0];
for(int i = 1, i < n, ++i) {
  SAT[i] = SAT[i-1] + Arr[i];
}
//Sum of a to b
float sum(int a, int b) { return SAT[b] - SAT[a-1]; }

  • in 2D: 第 \((i,j)\) 位存储 \((0,0)-(i,j)\) 的矩形区域和

    // m * n
for(int i = 0, i < n, ++i) {
  SAT[i][0] = Arr[i][0];
    for(int j = 1, j < n, ++j) {
        SAT[i][j] = SAT[i][j-1] + Arr[i][j-1];
    }
}
for(int j = 0, i < n, ++i) {
    for(int i = 1, j < n, ++j) {
        SAT[i][j] += SAT[i-1][j];
    }
}
//Sum of a to b
float sum(int a, int b) { return SAT[a-1][b] + SAT[a][b-1] - SAT[a-1][b-1]; }

Moment Shadow Mapping

VSSM Problem: 遮挡物简单情况下，遮挡深度分布非正态/不符合切比雪夫估计 ，估计值不准

  • 与实际值相比较暗：视觉无影响
  • 与实际值相比较亮：漏光（Light Leaking，工业界也有称Light Bleeding）

解决分布描述不准方法——引入高阶矩（Moments）

  • 简单理解为“ \(x^i\) 即 \(x\) 的 \(i\) 阶矩”
  • 使用前 \(m\) 阶矩的组合（ \(x^1,x^2,\dots,x^m\) ）可以描述一个具有 \(m/2\) 个“台阶”的阶跃函数
  • 可视为一种展开，将原函数展开为前 \(m\) 阶矩的线性组合
  • 在MSM中，前4阶矩可较好描述遮挡深度分布，在使用VSSM的想法计算所需值（可在Blocker Search和PCF环节使用该方法）

Distance Field Soft Shadows

Distance Field / Distance Function: Minimum distance to the closet location on an object SDF(Signed Distance Field) 是较好的混合方式，比线性插值得到结果更平滑连续——[ 最优传输理论 ]

Usages:

  • Ray marching (Sphere Tracing) 在某一点，作SDF值（距离物体的最小距离）为半径的球，则球体内任意方向发射光线均不与物体相交，将该半径定义为“安全距离”（safe distance）。则光线可以朝原方向走该半径长度的距离，得到新的点和SDF值，同理迭代。直到沿着同一方向与物体距离足够小，或光线路径过长（认为无物体与之相交）时停止追踪。 SDF1

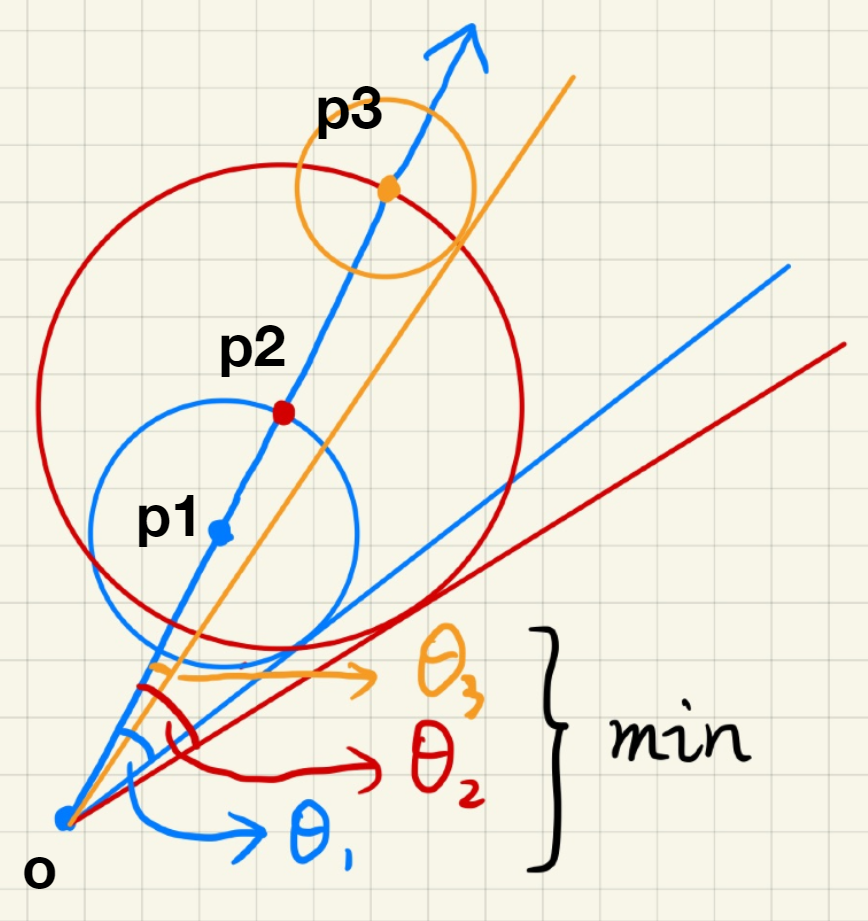
  • Soft Shadows 类Ray Marching，对每一根光线，算出”安全角度”（safe angle）。（光线上所有点的SDF值的最小值为半径，该点为圆心作圆，与光线发射点两条切线的夹角） \(\text{smaller safe angle}\Rightarrow\text{less visibility}\) SDF2 SDF3 \[ \begin{array}{l} \displaystyle V=\arcsin\frac{SDF(p)}{\|p-o\|}\quad \arcsin 计算量过大\\ \displaystyle V\approx \min\left\{\frac{k\dot SDF(p)}{\|p-o\|},1.0\right\}\quad 直接使用比值近似，其中k值决定过渡带宽度，即阴影软硬程度\\ \end{array} \]

  • 优势：快

  • 局限性：SDF的计算量、存储量，以及物体运动后重新计算的复杂度。（对多个物体的SDF，取最小值即可。）and some artifact

  • misc：利用SDF在实时渲染中生成矢量字符