2021-12-05-影片技术分析Pre-基于物理的动画-流体系统

流体系统

最后，在相对简单的前两个部分介绍后，我们还是不得不面对一个需要更多数学的系统，流体。

流体与流体力学

首先第一个问题是什么是流体。流体的定义是在承受剪应力（物体在外力作用时，内部任一截面上会出现的相互作用力，“内力”）时将会发生连续变形的连续介质，包括气体和液体。

• 所有液体
• 所有气体
• 具备流动特征的固体：如沙丘

流体主要具备以下性质：

• 流动性（fluidity）：流体间的分子作用力较小，难以保持一定的形状，在受到外界的作用力或能量不平衡时，流体会发生流动。

• 变形性（deformability）：在受到剪切力持续作用时，与固体的微小变形或有限变形不同，流体产生程度很大的、甚至作用时间无限长的变形。

• 粘性（viscosity）：相邻两层流体之间发生相对运动时，在两层流体的接触面会产生对于变形的抗力，与固体的摩擦力不同，这种抗力不与流体的变形大小有关，而与流体的变形速度正相关，这种抵抗变形的特性称为粘性。

  正相关的形式：

  • 线性相关 - 牛顿流体 \(\tau=\mu\dfrac{du}{dy}\)
  • 非线性相关 - 非牛顿流体 \(\tau=\mu(T,p)\left(\dfrac{du}{dy}\right)^2\)

• 可压缩性（compressibility）/不可压缩性（incompressibility）：在一定的温度下，单位压强增量引起的体积变化率定义为流体的压缩性系数(coefficients of compressibility)，其值越大，流体越容易压缩，反之，不容易压缩。

  在影视制作的物理模拟中，一般模拟的是不可压缩流体。

Navier-Stokes 方程

一般形式 \[ 动量方程\quad\displaystyle\underbrace{\frac{\mathrm D\mathbf u}{\mathrm Dt}}_{\frac{\partial\mathbf u}{\partial t}+\mathbf u\cdot\nabla\mathbf u}=\frac{1}{\rho}\nabla\cdot\underbrace\sigma_{应力加速度张量}+\mathbf g\\ 质量方程\quad\nabla\cdot\mathbf u=0 \]

不可压缩流体 Navier-Stokes 方程 \[ 动量方程\quad\displaystyle\overbrace{\underbrace{\frac{\partial\mathbf u}{\partial t}}_{非稳态加速度}+\underbrace{\mathbf u\cdot\nabla\mathbf u}_{对流加速度}}^{惯性加速度\frac{\mathrm D\mathbf u}{\mathrm Dt}}+\underbrace{\frac{1}{\rho}\nabla p}_{压强梯度}=\underbrace{\mathbf g}_{外力加速度}+\underbrace{\nu\nabla\cdot\nabla\mathbf u}_{粘滞力加速度(经常忽略)}\\ 质量方程\quad\nabla\cdot\mathbf u=0 \]

补充数学： \[ 哈密顿算子\quad\nabla=\left(\dfrac{\partial}{\partial x},\ \dfrac{\partial}{\partial y},\ \dfrac{\partial}{\partial z}\right)\quad\\ {\bf散度}\ \nabla\cdot \vec F\quad{\bf旋度}\ \nabla\times \vec F\ \\ 拉普拉斯算子\quad\Delta=\nabla\cdot\nabla=\nabla^2=\left(\dfrac{\partial}{\partial x},\ \dfrac{\partial}{\partial y},\ \dfrac{\partial}{\partial z}\right)^2\\ {\bf梯度}的{\bf散度}\ \Delta\vec F \]

流体模拟的两种视点

前面我们一直在用拉格朗日视点在考虑粒子和刚体的模拟，也就是“盯着运动物体看”。那在流体中，我们终于可以聊到两种视点。

流体是一种连续介质——什么叫连续介质，简单来说就是很难分割，你没法把一杯水分成一块一块的独立件去模拟，除非细到分子程度——我们的第一种思路就有点像：用超大规模的粒子去模拟流体。那就回归到了我们第一节课讲过的粒子系统，又由于粒子之间是要考虑相互作用力的，那么就是一个比较复杂的交互粒子系统。这就是我们流体模拟的拉格朗日方法。拉格朗日方法的优势在于非常直观，相对来说更加精确，但是问题是很难追溯流体中的某一部分，或者说某一区域的粒子，要选取范围来做粒子操作——永远需要遍历每一个粒子，需要用非常复杂的数据结构来优化。

另一种方法之前也给大家介绍过了：考虑空间网格而不是考虑单体的欧拉方法。在流体模拟中，也就是把流体运动的空间分割为网格，考虑每一个网格中是否有流体、流体的速度、加速度、受力等状态，然后迭代更新每一个网格的状态。欧拉方法则可以方便地调取某一区域的流体。后面会提到这个“方便调取”带来的优势。

近两年也出现了拉格朗日和欧拉的混合方法，就是一会拉格朗日、一会欧拉，来结合两者的优点。后面也会给大家介绍。

• 拉格朗日方法
• 欧拉方法
• 混合方法

拉格朗日方法：光滑粒子动力学

那么首先我们就为大家介绍一种最简单的拉格朗日流体模拟方法：SPH (Smoothed Particle Hydrodynamics)[2]。

SPH的核心思想就是把流体考虑成一个个相互作用的粒子：每一个粒子根据周围一定范围的粒子的位置、受力、粘力等状态来更新自己的状态，从而计算出加速度和速度，进行反复迭代。

首先我们来解释一下“光滑”的概念。先给大家讲一种比较形象的解释方式，两个小球，不接触（手做演示）时互不影响，一旦接触就反弹，这叫不光滑；而如果这两个小球接触时不会立即弹开，而是有一个缓冲，先接触、重合然后慢慢地弹开，就叫做光滑。严谨的表述是，两个粒子的相互影响在相近一定距离时发生（接触），相互影响的程度随着距离的接近从0开始逐渐增大（缓冲），即形成下图右图这样的相互影响程度 - 距离函数，我们称之为光滑核函数。

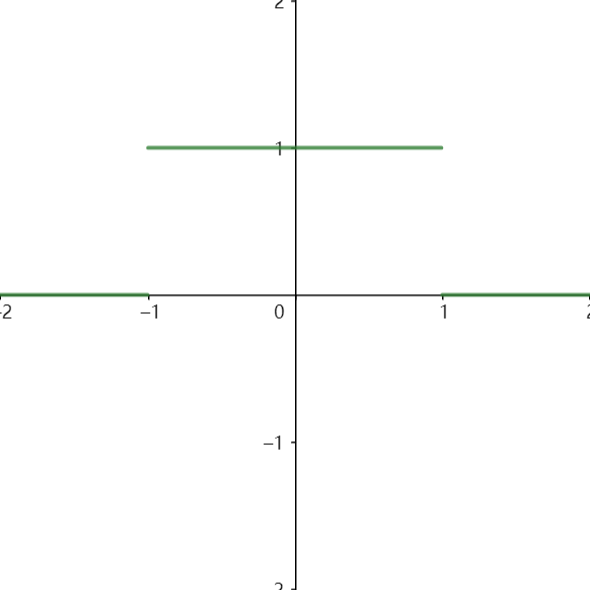
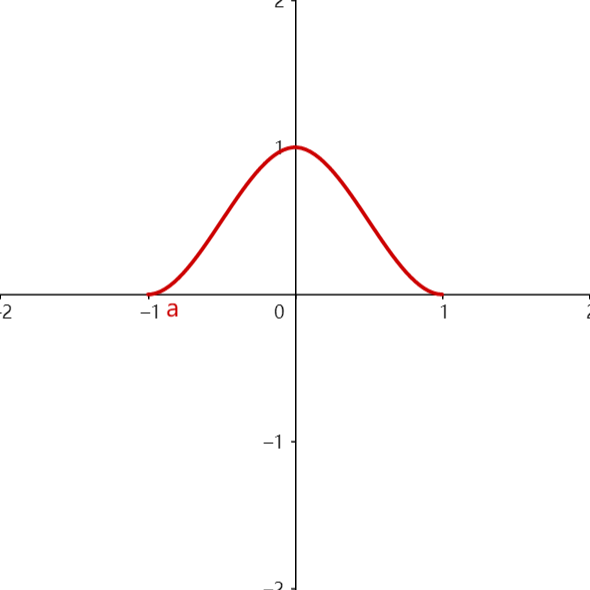
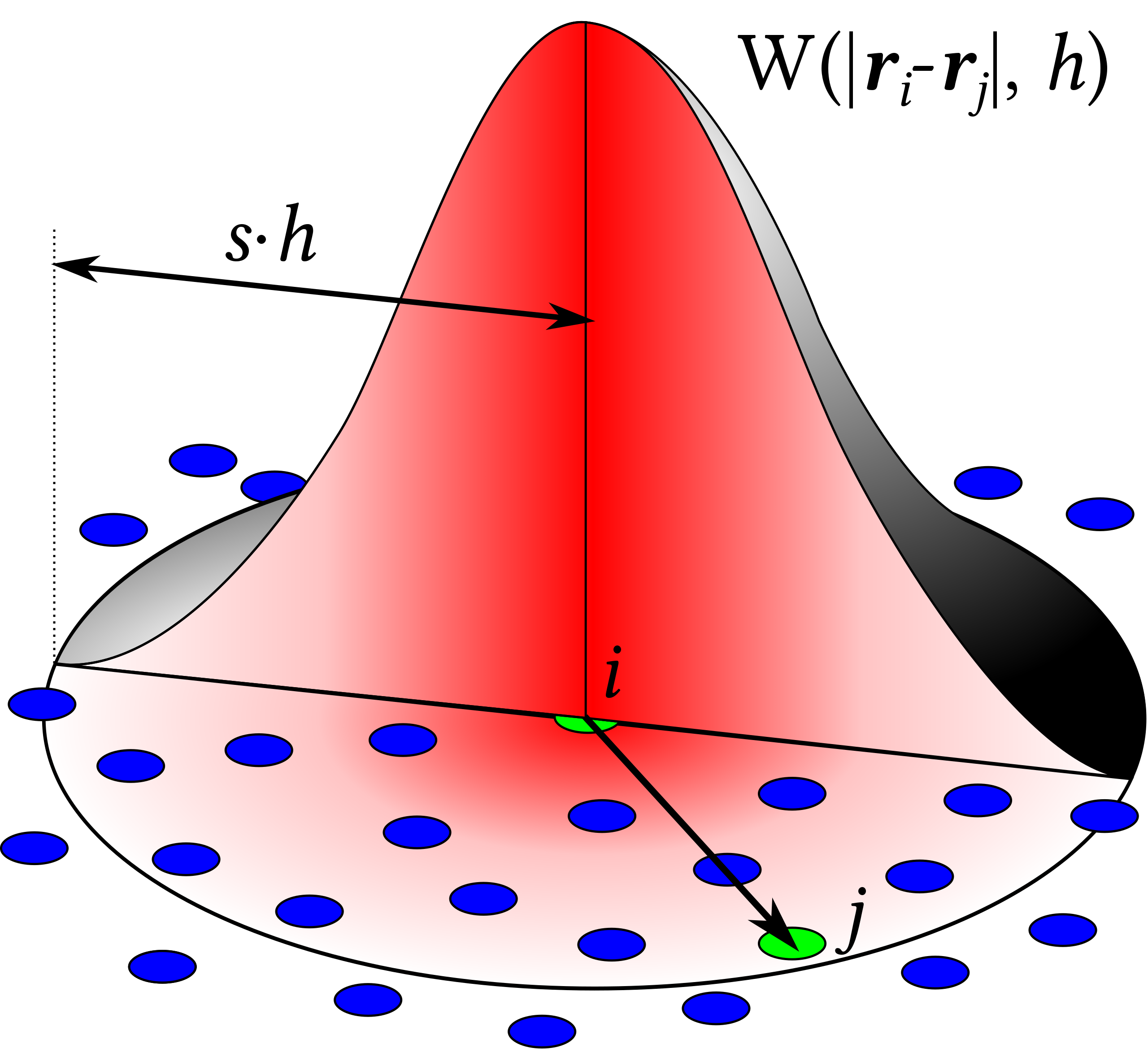
设第 \(i\) 个粒子的坐标是 \(\mathbf x_i\) ，对空间中任一点 \(\mathbf x\) ， \(\mathbf r =\mathbf x - \mathbf x_i\) ，核函数即为： \[ \omega_i(\mathbf r)=\omega(\|\mathbf r\|)\\ \]

“最大半径”的概念我们也称为有限支撑，设该最大半径/有限支撑为 \(r_{max}\) 。 \[ r\ge r_{max}时,\quad\omega(r)=0\\ \oint \omega_{(r)}d\mathbf r=1 \]

光滑核函数选择是很多的，只要满足以上条件的函数都可以用于核函数，一般根据我们的动画需要来选择，也可以根据动画效果来做一些参数的调整。可以是我们上图中这样的，也可以是接近0时趋向正无穷的。

那么有空间中的任意场 \(A\) 、场梯度 \(\nabla A\) 及密度 \(\rho\) 计算方法分别为： \[ A(\mathbf x)=\sum_i A_i \dfrac{m_i}{\rho_i}\omega(\|\mathbf x-\mathbf x_i\|),\quad\rho_i=\sum_j m_j\omega(\|\mathbf x_i-\mathbf x_j\|)\\ \nabla A_i=\rho_i\sum_j m_j\left(\dfrac{A_i}{\rho_i^2}+\dfrac{A_j}{\rho_j^2}\right)\nabla_{\mathbf x_i}\omega(\|\mathbf x_i-\mathbf x_j\|)\quad (\nabla_{\mathbf x_i}\omega指核函数在位置{\mathbf x_i}的梯度) \]

则我们就可以来做最简单的SPH算法了：WCSPH (Weakly Compressible SPH)。最终在程序中每一个时间步的计算步骤为：

• 对于每个粒子 \(i\) ，计算其密度 \(\rho_i\) ，从而得到压强 \(p_i\) ，进一步计算得到压强梯度 \(\nabla p_i\) ： \[ \rho_i=\sum_j m_j\omega(\|\mathbf x_i-\mathbf x_j\|)\\ p_i=B((\dfrac{\rho_i}{\rho_0})) \]

• 对于每个粒子 \(i\) ，计算所在位置的压强梯度 \(\nabla p_i\) ，即： \[ \nabla p_i=\rho_i\sum_j m_j\left(\dfrac{p_i}{\rho_i^2}+\dfrac{p_j}{\rho_j^2}\right)\nabla_{\mathbf x_i}\omega(\|\mathbf x_i-\mathbf x_j\|) \]

• 代入N-S方程（忽略了粘度项 \(\nu\nabla\cdot\nabla\mathbf u\) ），计算每个粒子 \(i\) 的材料加速度 \(\dfrac{\mathrm D\mathbf u}{\mathrm Dt}\) ，从而直接计算当前时间步的速度与位移： \[ a=-\dfrac{\nabla p}{\rho}+g\\ 以显式时间积分方法为例\quad\begin{array}{l}\mathbf v_{t+1}=\mathbf v_t+\Delta t\left(-\dfrac{\nabla p}{\rho}+\mathbf g\right)\\ \mathbf x_{t+1}=\mathbf x_t+\Delta t\mathbf v_{i+1}\end{array} \]

除了我们最简单的WCSPH，还有一些拓展方法。

• WCSPH, Weakly Compressible SPH 最简单的显式求解
• PCISPH, Predictive-Corrective Incompressible SPH 不断调整压力值控制密度，保证不可压缩性，循环修正过程即为“预估矫正 (Predictive-Corrective)”
• IISPH, Implicit Incompressible SPH 隐式求解，使用 Relaxed Jacobi Method 求解，PCISPH
• DFSPH, Divergence-Free SPH 不仅保证密度恒定，还要保证速度的散度为0

如这张图中的效果就是PCISPH方法在二维中的一个呈现，通过Taichi编程显示。

SPH方法的优势在于理解起来相对简单，再加以一定的条件后也能够达到相当的精确性。但SPH方法在粒子量较大时计算会比较慢，尤其是在搜索附近粒子时没有很好的加速方法的话。此外，SPH想要保证流体的不可压缩性，只能通过PCISPH那种预估矫正的方法来保证。

案例分享

近年来，SPH方法主要还是用于建筑、桥梁等土木工程流体仿真计算中，在电影中应用较少。我能搜到的一个应用粒子是《超人：英雄归来》中，Tweak (Shotgrid) 在一些流体镜头中应用了SPH方法。

欧拉方法：Stable Fluids

纯拉格朗日方法有什么问题呢？前面我们提到过，我们无法对其中某些部分粒子单独操作，一旦模拟开始了，就无法控制，只能通过初始参数的设定来调整效果。我们看一个欧拉方法的案例：WebGL2-StableFluids。在网格化的方法中，我们就能比较方便地操作某一个区域的流体——网格是固定不动的，这一时间步的 \((0.5,0.5)\) 和下一时间步的都是指的同一个网格。

在欧拉方法中，我们不再关注流体本身，而是关注流体流过的空间。那么我们就要把前面用到的材料导数拆开： \(\displaystyle \frac{\mathrm D\mathbf u}{\mathrm Dt}=\frac{\partial\mathbf u}{\partial t}+\mathbf u\cdot\nabla\mathbf u\) ，我们现在要在网格里存的是 \(\dfrac{\partial\mathbf u}{\partial t}\) ，也就是我们比起拉格朗日方法直接得到 \(\dfrac{\mathrm D\mathbf u}{\mathrm Dt}\) ，现在要多计算 \(-\mathbf u\cdot\nabla\mathbf u\) 这一项了，这一项叫做对流项。

我们这里用欧拉方法中最经典的一篇Paper，Stable Fluids[3]的实现为例来讲解欧拉方法的细节，Stable Fluids把N-S方程先做了一个变形： \[ \displaystyle\frac{\partial\mathbf u}{\partial t}=-\frac{1}{\rho}\nabla p-\mathbf u\cdot\nabla\mathbf u+\nu\nabla\cdot\nabla\mathbf u+\mathbf g\\ \Rightarrow\quad\displaystyle\frac{\partial\mathbf u}{\partial t}=\mathbf P(-\mathbf u\cdot\nabla\mathbf u+\nu\nabla\cdot\nabla\mathbf u+\mathbf g)\\ (\mathbf P 表示压强的投影算子，消去了单独的压强项-\frac{1}{\rho}\nabla p) \] 在拉格朗日方法中，我们把粒子的所有受力计算出来、叠加得到合力，最后再来做时间积分的。然而欧拉方法中我们是逐项逐步来做计算，每一步得到一次速度，每一步的输出要作为下一步的输入，如下图依次执行。

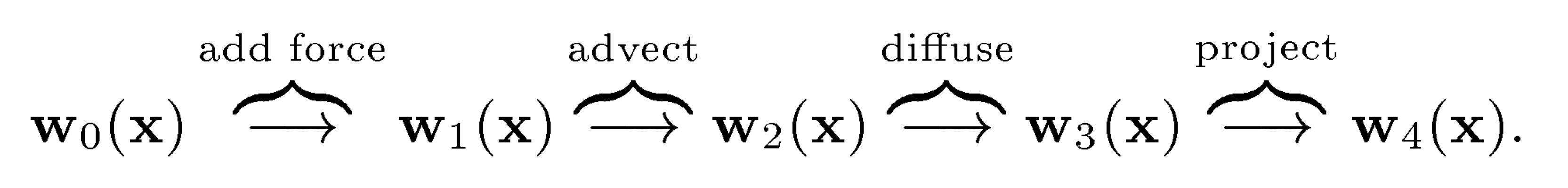
• Add force 处理统一的外力，这一步相对简单，就是给流体一个统一的外力，比如重力
• Advection 步进，计算对流项 \(-\mathbf u\cdot\nabla\mathbf u\) ，更新粒子速度和位置。
• Diffusion 耗散，计算粘度项 \(\nu\nabla\cdot\nabla\mathbf u\) ，这一条我们在这次讲解中就简单带过了，一般在模拟高粘度的流体比如胶水时，才比较需要这一项。
• Projection 投影，计算投影算子 \(\mathbf P\) 或者压强项 \(-\dfrac{1}{\rho}\nabla p\) 。

在具体讲解之前呢，我们还是先了解一下，“网格化”的一些细节。网格化本身是一个很容易的事情，能够产生不一样的地方在于，我们怎样存储网格化的流体的状态。

• 最简单的一种方式就是我们把所有属性：速度、压强存在每一个网格的中心；
• 另一种稍微复杂一些的方式是我们把压强存在网格的中心，而把速度拆成垂直分量和水平分量，分别存储在网格的左右两边中点和上下两边中点，这种方式我们也称为MAC网格。 这样能够避免掉简单的中心存储可能出现的“棋盘格图案 Checkerboard Pattern”。

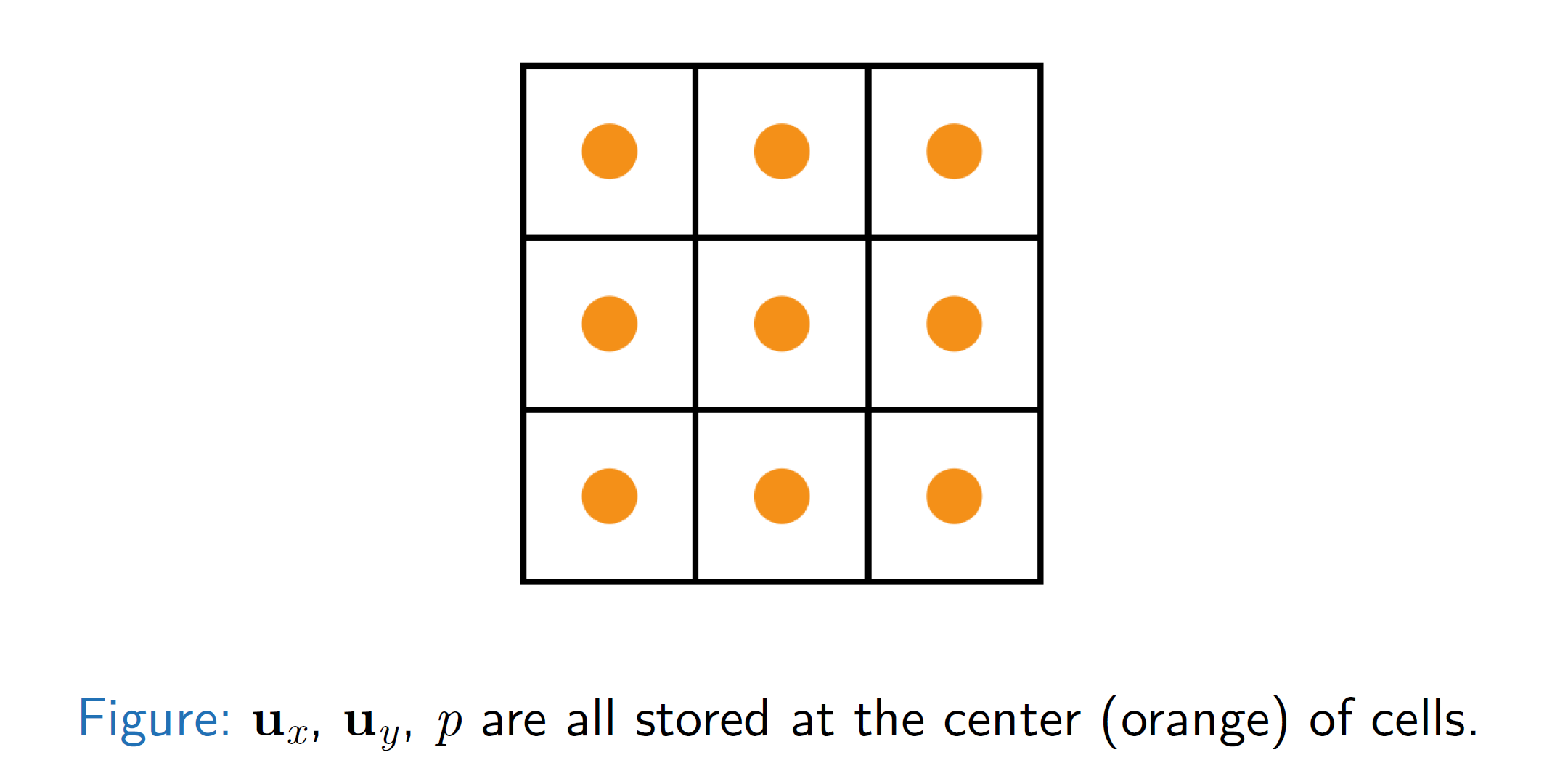
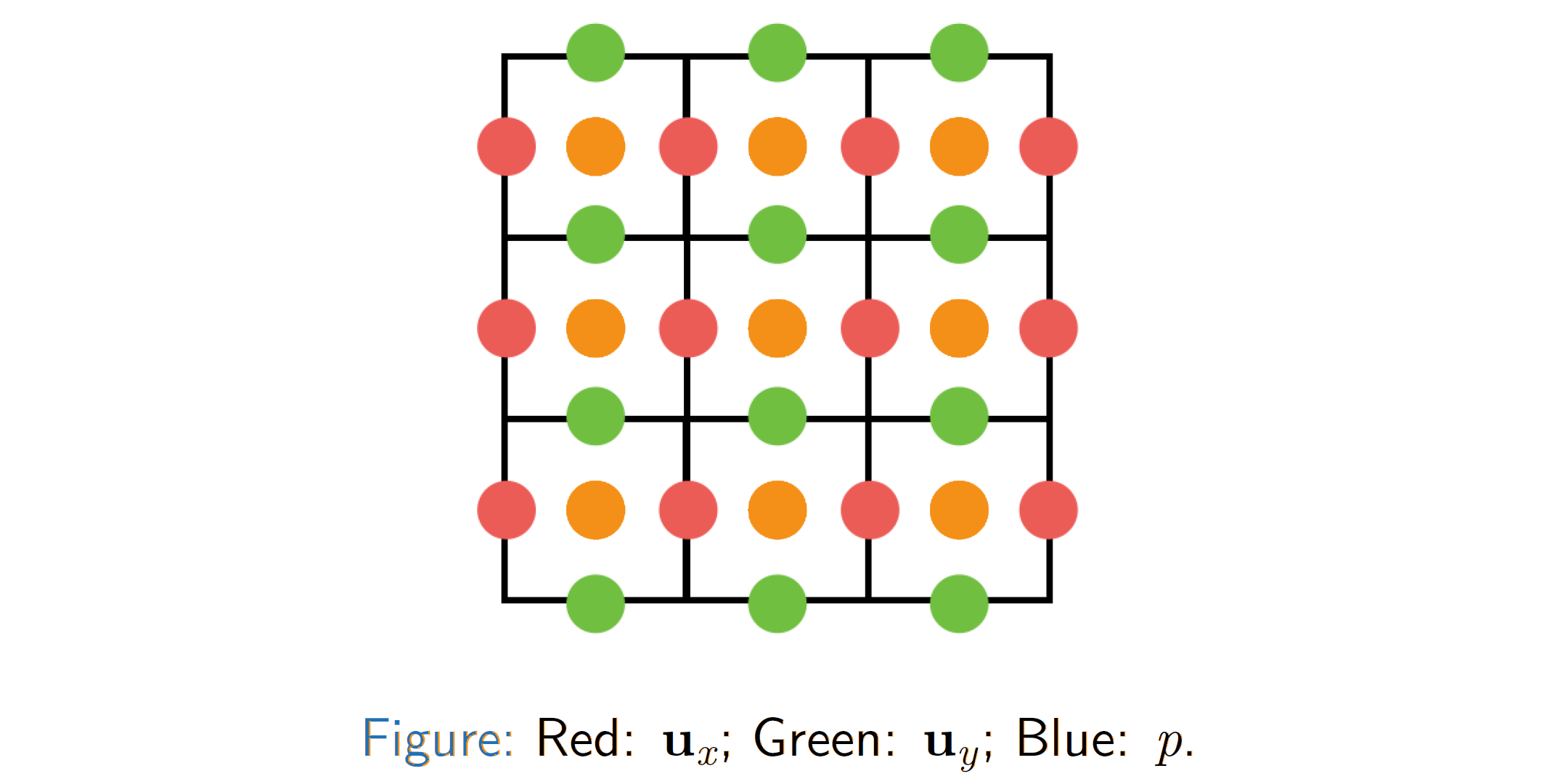
Grid

在这个基础上，我们的下一个问题是，我在空间中任意取一点并不在网格存储点位置的点，怎样去求其状态——这里我们使用的就是简单的双线性插值。就像下图，用它周围的四个点的状态计算、用面积作为权重。

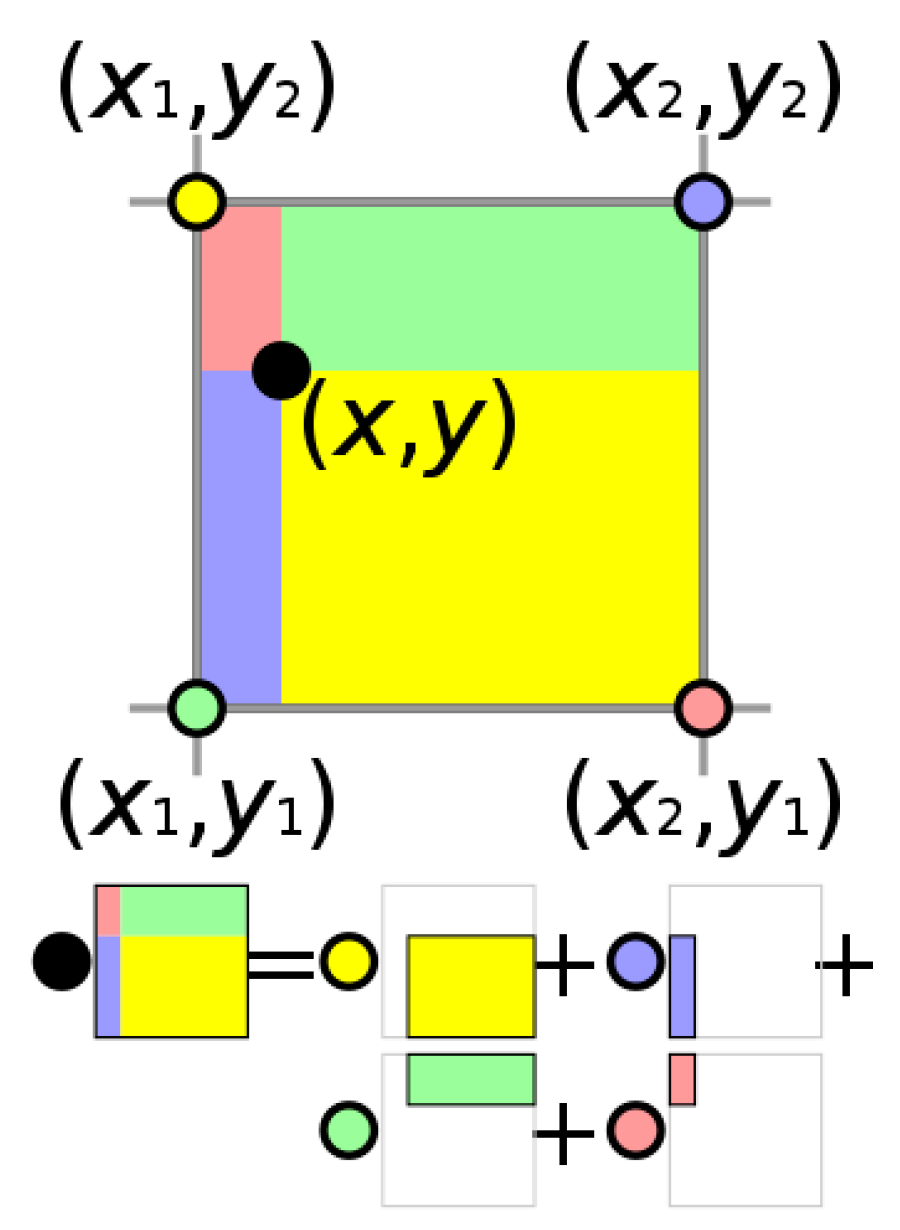
Advection

在计算对流项这一步，Stable fluid实现的方法被称为半拉格朗日法，为什么又要“拉格朗日”？

我们考虑某一个网格位置当前的速度是什么？这里我们用粒子来考虑：就是一个粒子从上一个地方流到了这一个地方——就是粒子在的上一个地方的速度（要注意，我们这里计算的是对流项，因此不考虑压强带来的速度变化）。那Advection的思路就出来了：

如下图，首先假定一个网格中心 \(\mathbf x\) 处存在粒子 \(p\) ，由处当 \(p\) 前的速度 \(\mathbf u\) 反向追溯得 \(p\) 前一个时间步的位置 \(\mathbf x_{old}\) ，这个 \(\mathbf x_{old}\) 就不一定在网格中心了，用它周围的速度场插值得到它的速度 \(\mathbf u_{old}\) 也就是我们要更新的 \(\mathbf u_{new}\) 。

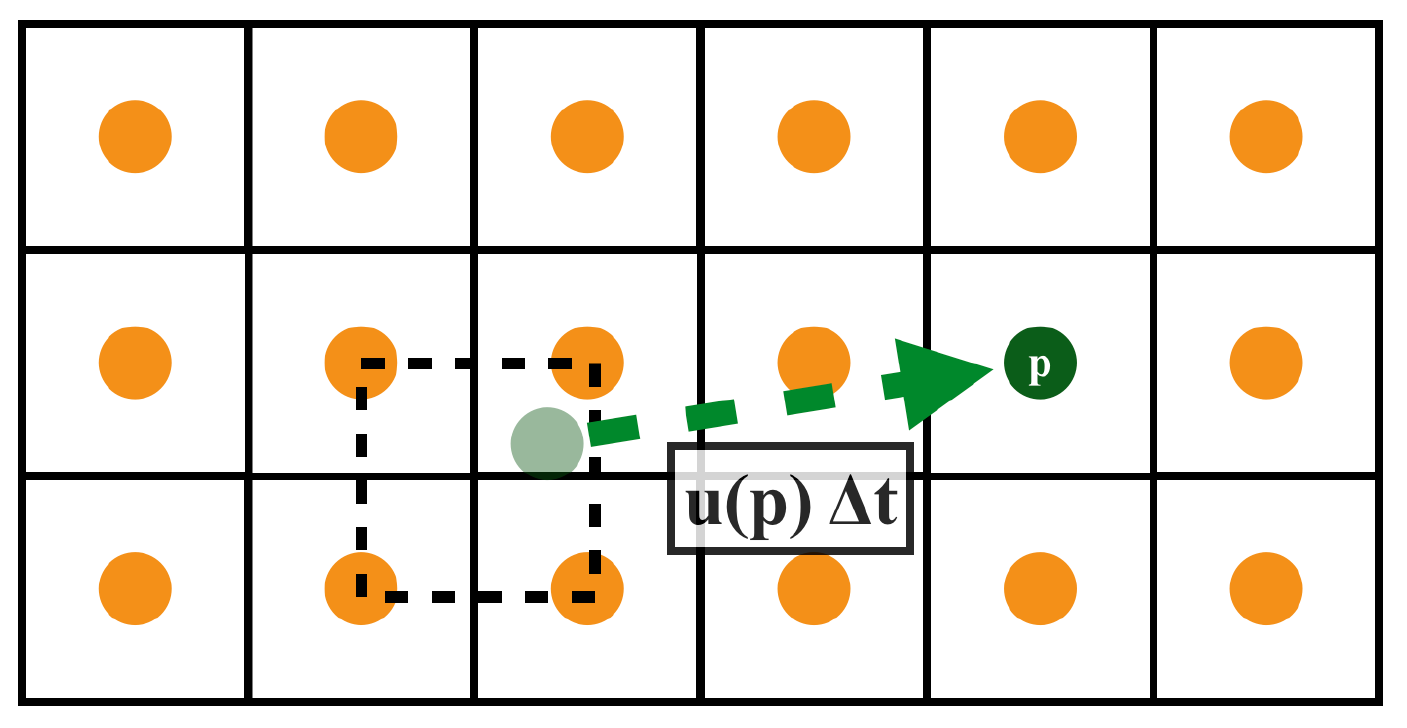
但是这时可能会存在下图这种现象，尤其是时间步长较大时非常明显：运动方向与我们的追溯方向偏差较大，不断地偏差下去就会一次比一次大，最终出现整个流体速度场的整体性偏移。那么怎么解决它呢：

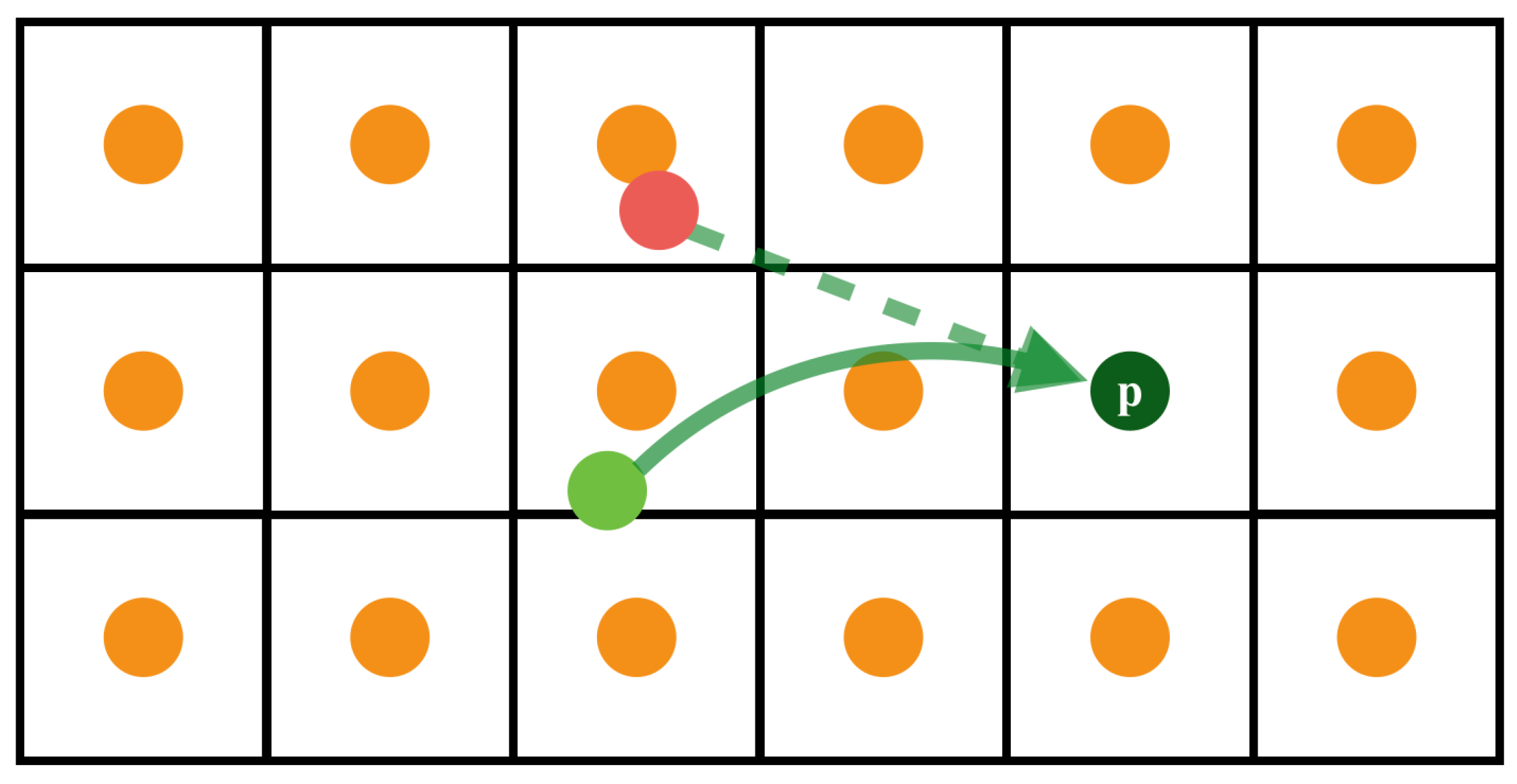
那根据我们之前做正向速度更新时的经验，我们就可以“往回走两步”，或者说是“先走半步、再走半步”，即我们熟悉的“中点法”，这样我们就能够追溯地更加精准。当然也可以走三步，相对来说就没那么必要了。这个过程，其实本质上是在解非线性常微分方程的数值解，用的方法叫做Runge-Kutta方法，我们最简单的走一步就是RK1，走两步就是RK2，三步就是RK3方法。

此外呢，在插值问题上，后来也有人用样条插值（比如Catmull-Rom）来对线性插值做改进。

Diffusion

Diffusion这一步相对简单，如果要做的话。我们就直接逐网格求得粘度加速度，再在Advection得到的速度基础上做时间积分即可。 \[ \dfrac{\partial\mathbf u}{\partial t}=\nu\nabla^2\mathbf u \] 以简单的前向时间积分为例就是： \[ \mathbf u^{n+1}=\mathbf u^n+\Delta t \nu\nabla^2\mathbf u^n \] 当然，这个前向时间积分也可以用隐式的时间积分方法（比如后向欧拉）来完成，Stable Fluids就是把上面这个计算过程换成用后向欧拉方法、使用共轭梯度法迭代来计算的，这里我们就省略过程了。

Projection

在Projection这一步，我们求的其实是压强，压强这一项其实是为了保证流体的不可压缩性，因此我们有条件：速度的散度为0。我们这一步的条件其实就是： \[ \dfrac{\partial\mathbf u}{\partial t}=-\dfrac{1}{\rho}\nabla p\ ,\quad\nabla\mathbf u=0 \] 那么我们用后向欧拉的思路就得到了压强的泊松方程（Pressure Poisson equation, PPE）： \[ \mathbf u^{n+1}-\mathbf u^n=-\Delta t\dfrac{\nabla p}{\rho}\ ,\quad \nabla\mathbf u^{n+1}=0\\ \Rightarrow\ 泊松方程\ \nabla\cdot\nabla p=\dfrac{\rho}{\Delta t}\nabla\cdot\mathbf u \] 我们用中心差分方法代替其中的哈密顿算子和拉普拉子算子后，这个泊松方程又是一个形如 \(Ax=b\) 的超大规模线性方程，我们用各种迭代方法去解它就好了。 \[ \begin{aligned}(\mathbf Ap)_{i,j,k}&=(\nabla\cdot\nabla p)_{i,j,k}\\&=\dfrac{1}{\Delta x^2}(-6p_{i,j,k}+p_{i+1,j,k}+p_{i-1,j,k}+p_{i,j+1,k}+p_{i,j-1,k}+p_{i,j,k+1}+p_{i,j,k-1})\\\\ \mathbf b_{ij}&=\left(\dfrac{\rho}{\Delta t}\nabla\cdot\mathbf u\right)_{i,j,k}\\&=\dfrac{\rho}{\Delta t\Delta x}(\mathbf u_{i+1,j,k}^x- \mathbf u_{i,j,k}^x+\mathbf u_{i,j+1,k}^y-\mathbf u_{i,j,k}^y+\mathbf u_{i,j,k+1}^z-\mathbf u_{i,j,k}^z)\end{aligned} \] 不过这里的 \(A\) 是一个超大规模的稀疏对称正定矩阵（ \(nml\times nml,\ nml\ 分别为\ xyz\ 方向的网格数量\) ），我们也会有一些计算方法去优化它。

不过在烟雾这样的流体模拟中，温度也会带来变量。因此在模拟烟雾等流体时，压强场的泊松方程还需要做一些小变化：密度 \(\rho\) 不是固定的了，针对每一网格要通过温度去计算浮力、从而得到新的 \(\rho\) 来参与计算。这里不再赘述。

案例分享

欧拉方法在混合方法出现之前，一度是电影工业界最流行的模拟方法。这里给大家讲一个趣事，就是我们前面分析的Stable Fluids这篇paper，刚投递到Siggraph时，审稿人直接给毙了：这写的什么东西啊，尤其是对它用半拉格朗日法求对流项速度的方法意见颇大——也太不精确了。但是很快，这一方法就在工业界被大量使用了：我们电影、游戏要多少物理精确啊，速度快、好看、好用才是对的。因此直到这一方法已经几乎成为工业界的成熟方案，才被会议接收发表。

欧拉方法非常适合用于烟雾、火焰等流体的模拟，我们利用Houdini中的Pyro工具架也制作了一个简单的烟雾模拟DEMO：给大家演示一下。

混合欧拉-拉格朗日方法

整体上来说，一个流体模拟系统总体来说大致主要就是Advection（步进：根据速度更新粒子状态或进行场的流动）和Projection（投影：更新速度，维持物质守恒/不可压缩性）两步。在拉格朗日方法的SPH中，我们虽然没有强调这两个概念，因为Advection步骤很轻松就完成了，但是Projection时需要复杂的数据结构（或者逐个遍历）来实现邻域的访问，因此很难保证流体的不可压缩性——直到PCISPH中引入了一个有点复杂的预估校正系统才能保证这一点。而在欧拉方法中的Advection步骤中却很难精确地处理场的流动，我们用RK2甚至RK3才能够消除误差，甚至还不能完全消除图形上的Artifact，而且很容易丢失能量和几何的细节；Projection却因为我们可以很方便地调取周边网格的状态变得非常好操作。所以我们就想，能不能将这两个方法混合一下。

当然可以，那么这类混合方法的思路就是：在粒子上做速度与状态更新，在网格上做压强计算与边界条件处理。算法的核心是 P2G 和 G2P 两个函数，分别是把粒子上的信息转换到网格上和把网格上的信息转换到粒子上，然后在粒子上和网格上分别做适合的工作。

• Particle to Grid transfer (P2G)
• Grid Operation
  • Pressure projection
  • Boundary conditions
  • …
• Grid to Particle transfer (G2P)
• Particle operation
  • Move particles
  • Update material
  • …

PIC, Particle in Cell 粒子元胞法

那么我们以最古老也最简单的一种混合欧拉-拉格朗日方法：PIC[4]，Particle in Cell，粒子元胞法为例，先给大家介绍 P2G 和 G2P 两个函数的实现。

从这两张图就可以清晰地看到 P2G 和 G2P 的过程。

• 我们通常先选择一个网格范围，这里是二维的 \(3\times 3\) 的网格，作为 P2G 或 G2P 中的网格作用范围，把粒子的状态“摊”到这些网格上或者是把这些网格的状态收集起来作为粒子的状态。
• 这里我们就会又一次用到前面介绍的“核函数”。这里粒子对每一个网格、每一个网格对粒子的“贡献”是不一样的，所以我们在“分摊”或者“收集”时要用一个权重，这个权重就是我们关于距离的核函数 \(\omega\|\mathbf x_i-\mathbf x_p\|\) 。

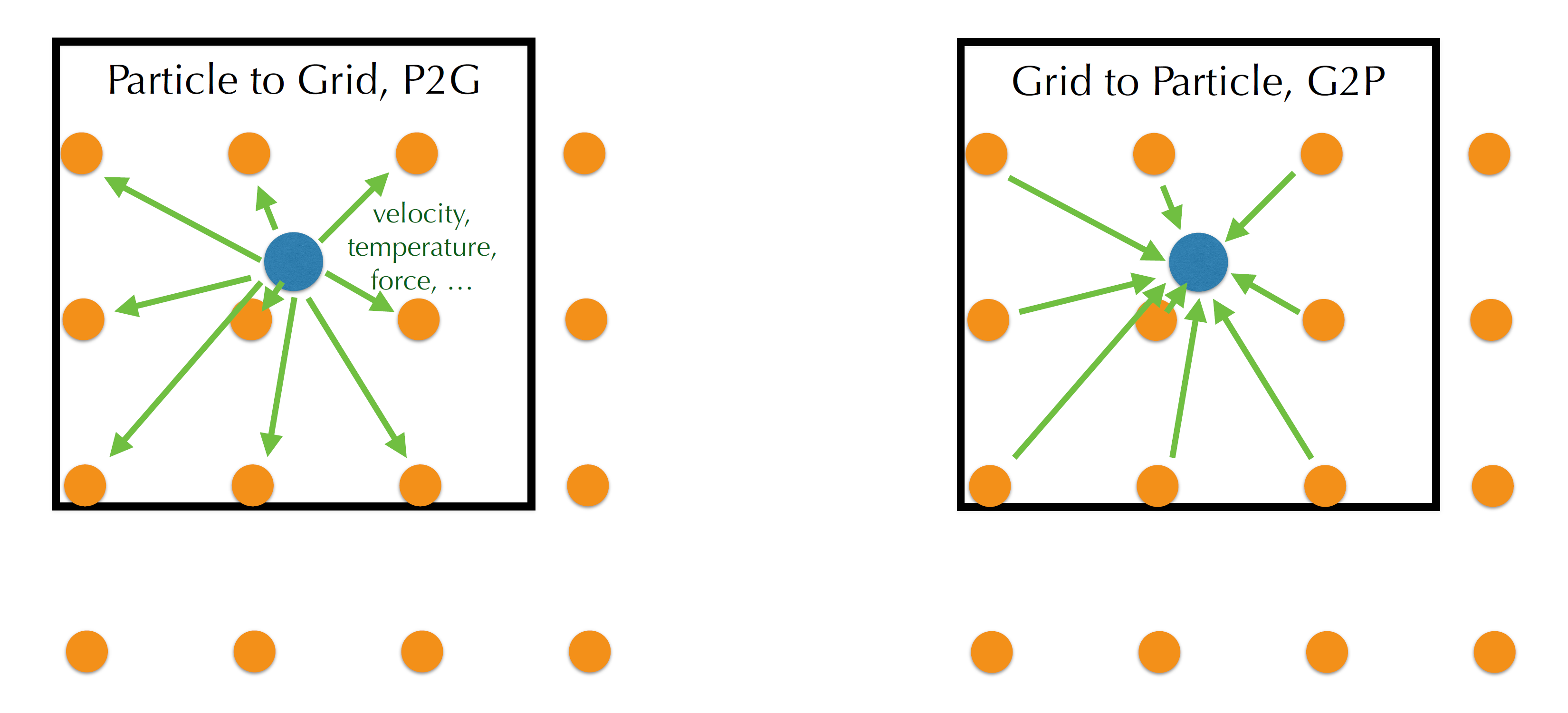
那么我们就可以实现我们的想法：在网格中做Projection（就如欧拉方法中那样），在粒子中做Advection（直接使用粒子携带的速度值移动）了。程序变得简单了起来（二维）：

# P2G
for p in x:
    base = (x[p] * inv_dx - 0.5).cast(int)
    fx = x[p] * inv_dx - base.cast(float)
    # Quadratic B-spline
    w = [0.5 * (1.5 - fx) ** 2, 0.75 - (fx - 1) ** 2, 0.5 * (fx - 0.5) ** 2]
    for i in ti.static(range(3)):
        for j in ti.static(range(3)):
            offset = ti.Vector([i, j])
            weight = w[i][0] * w[j][1]
            grid_v[base + offset] += weight * v[p]
            grid_m[base + offset] += weight
# Grid normalize
for i, j in grid_m:
    if grid_m[i, j] > 0:
        inv_m = 1 / grid_m[i, j]
        grid_v[i, j] = inv_m * grid_v[i, j]

# G2P
for p in x:
    base = (x[p] * inv_dx - 0.5).cast(int)
    fx = x[p] * inv_dx - base.cast(float)
    # Quadratic B-spline
    w = [0.5 * (1.5 - fx) ** 2, 0.75 - (fx - 1.0) ** 2, 0.5 * (fx - 0.5) ** 2]
    new_v = ti.Vector.zero(ti.f32, 2)
    for i in ti.static(range(3)):
        for j in ti.static(range(3)):
            weight = w[i][0] * w[j][1]
            new_v += weight * grid_v[base + ti.Vector([i, j])]
    x[p] = clamp_pos(x[p] + v[p] * dt)
    v[p] = new_v

但是这种方法有一个什么问题呢？试想如果同一个 \(3\times 3\) 网格中有两个粒子，它们的速度都被均摊到了这九个网格上，在迭代完成后再次从这九个网格中收集到新的速度时，A粒子的新速度就包含了B粒子的旧速度的一部分，同理B也是——因此，在不断地迭代过程中，其实是一个速度的细节丢失、不断平均化的过程——尤其是旋转、拉伸等运动，动着动着可能就停下来了。

换一种理解方式，我们的二维中9个网格有18个运动的自由度（每个网格xy两个方向），而转换到的粒子却只有2个移动的自由度，如果是三维的话这个数字会是：81/3——因此信息就会丢失掉非常多。

所以人们就带来了新的思路，主要分为这两类：

• APIC、PolyPIC：让粒子携带更多自由度的信息
• FLIP：不直接传递值，而是传递前后时间步的差分或物理量的梯度/倒数

APIC, Affine Particle in Cell

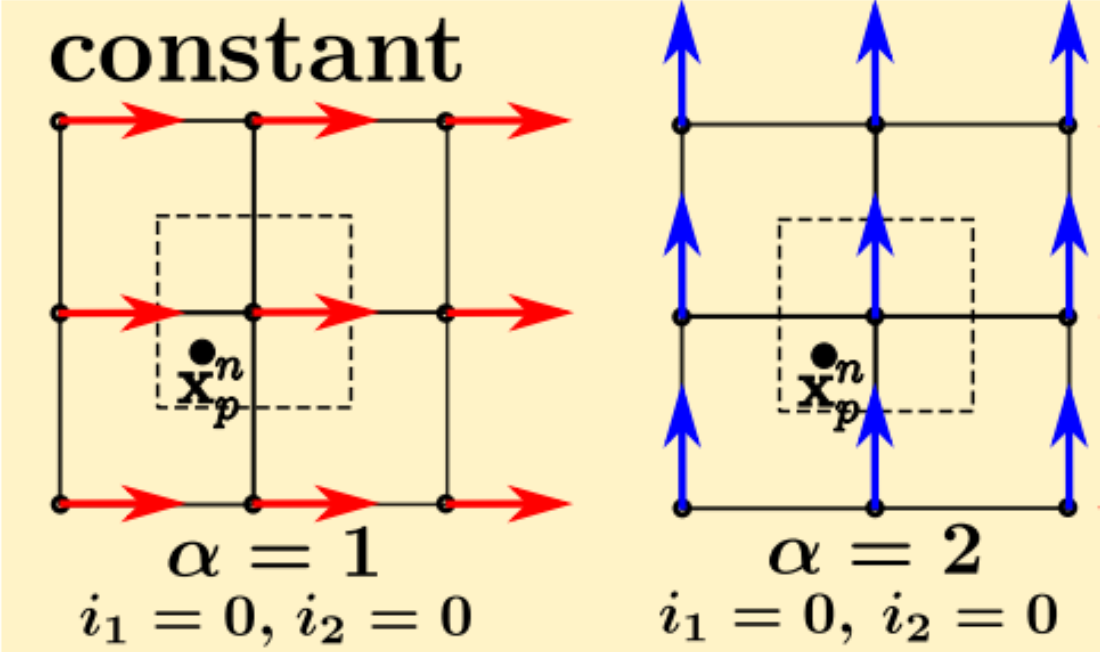
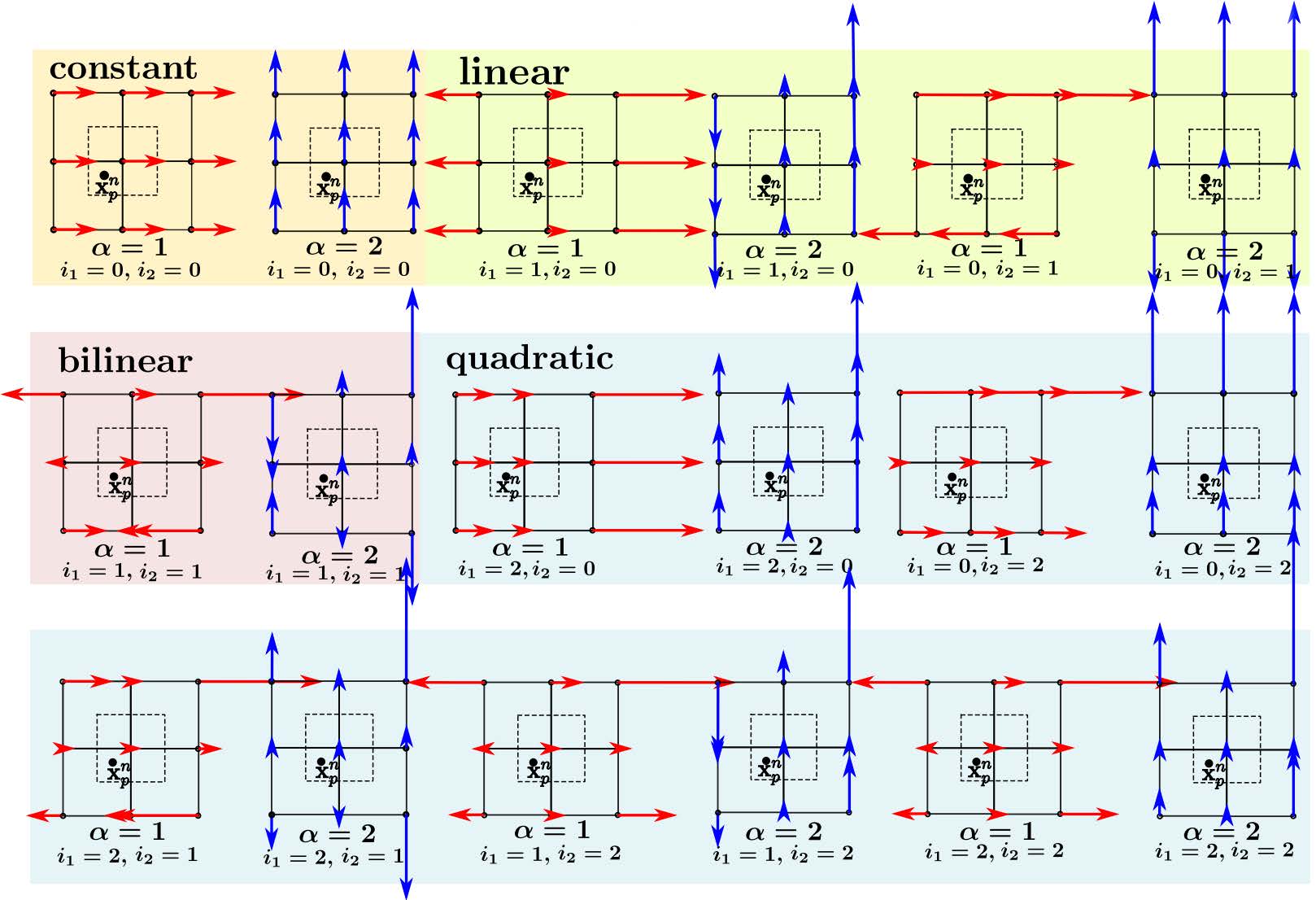
第一种思路我们先说说APIC[5]。APIC其实就是通过给粒子增加一个Affine矩阵，来存储粒子的更多种速度信息——网格的不同自由度的作用中，就有下图（二维）这几种，刚好可以通过仿射变换包含进来。从而就将粒子的自由度拓展为原来的三倍，二维中就是6自由度，三维就是9个。

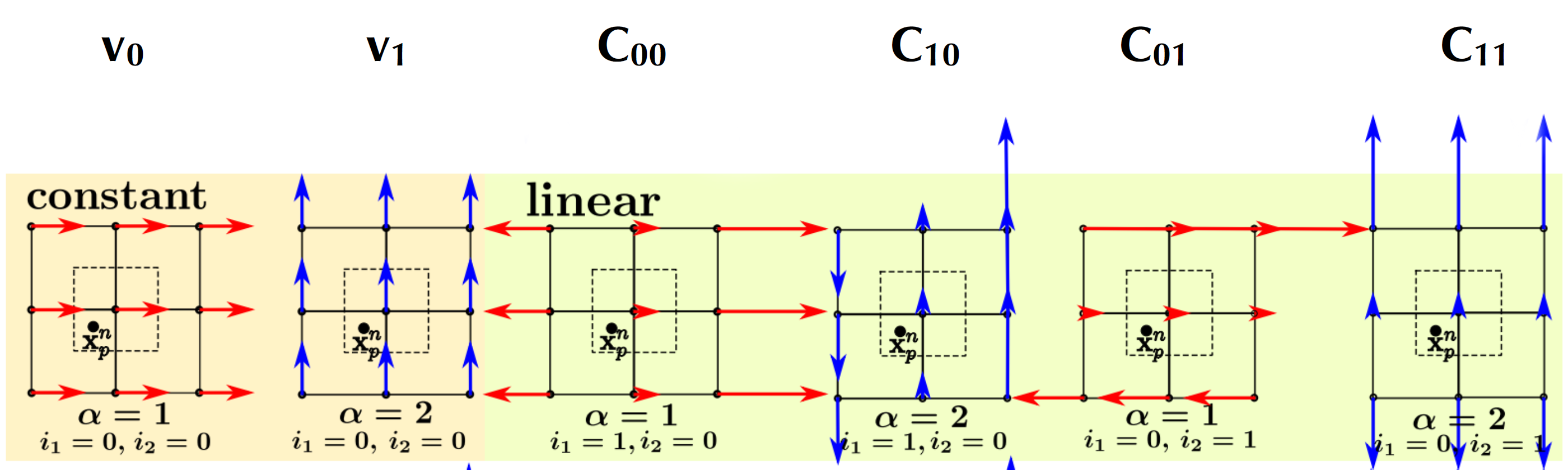
当然这个方法还涉及到怎样来计算这个Affine矩阵的问题，数学推导非常复杂就不给大家讲解了。代码实现却非常简单：用一个张量积来计算这个Affine矩阵即可。也不演示了。效果上带来的区别非常明显：流体可以正常的旋转、拉伸、剪切运动了。

而PolyPIC[6]则是进一步拓展了粒子的自由度——达到与网格一样的级别，当然复杂度也进一步提升了。

APIC也逐渐在影视制作中使用，尤其适合海洋、瀑布等水体的模拟，在迪士尼影片《海洋奇缘》中就有应用。

FLIP, Fluid Implicit Particles 隐式粒子流体法

影视工业目前最常用的方法

FLIP方法[7][8]的核心想法在于，我们不把表述粒子状态的物理量直接与网格传递，而是传递一个时间步里的增量。

还是以速度为例，我们在PIC系列方法中的 P2G 是 \[ \mathbf v_p^n={\rm gather}(\mathbf v_i^n) \] 而FLIP方法中，则 \[ \mathbf v_p^{n+1}={\rm gather}(\mathbf v_i^{n+1}-\mathbf v_i^n) \] 这样，A粒子中包含B粒子的速度成分就只有B粒子速度对加速度的一点点影响，而不会被“平均”掉了。

但是FLIP方法中，由于加速度的因素“成分”和原速度“成分”不一致，最终得到的结果会有很大的噪声——大家可以看到：毛毛刺刺的。到这里呢，我们刚好可以做一个多种常用模拟水的流体方法的对比（欧拉、PIC、APIC、FLIP）：

那么怎么办呢：非常简单，我们把PIC方法和我们的FLIP做一个Blend，而且这个比例呢只需要混一点点PIC，可以通过这个网站例子来玩一下GPU-based Fluid Simulation (yuanming-hu.github.io)： \[ \rm FLIP0.99=0.99*FLIP+0.01*PIC \] 这是跟前面对比的FLIP0.97方法的效果

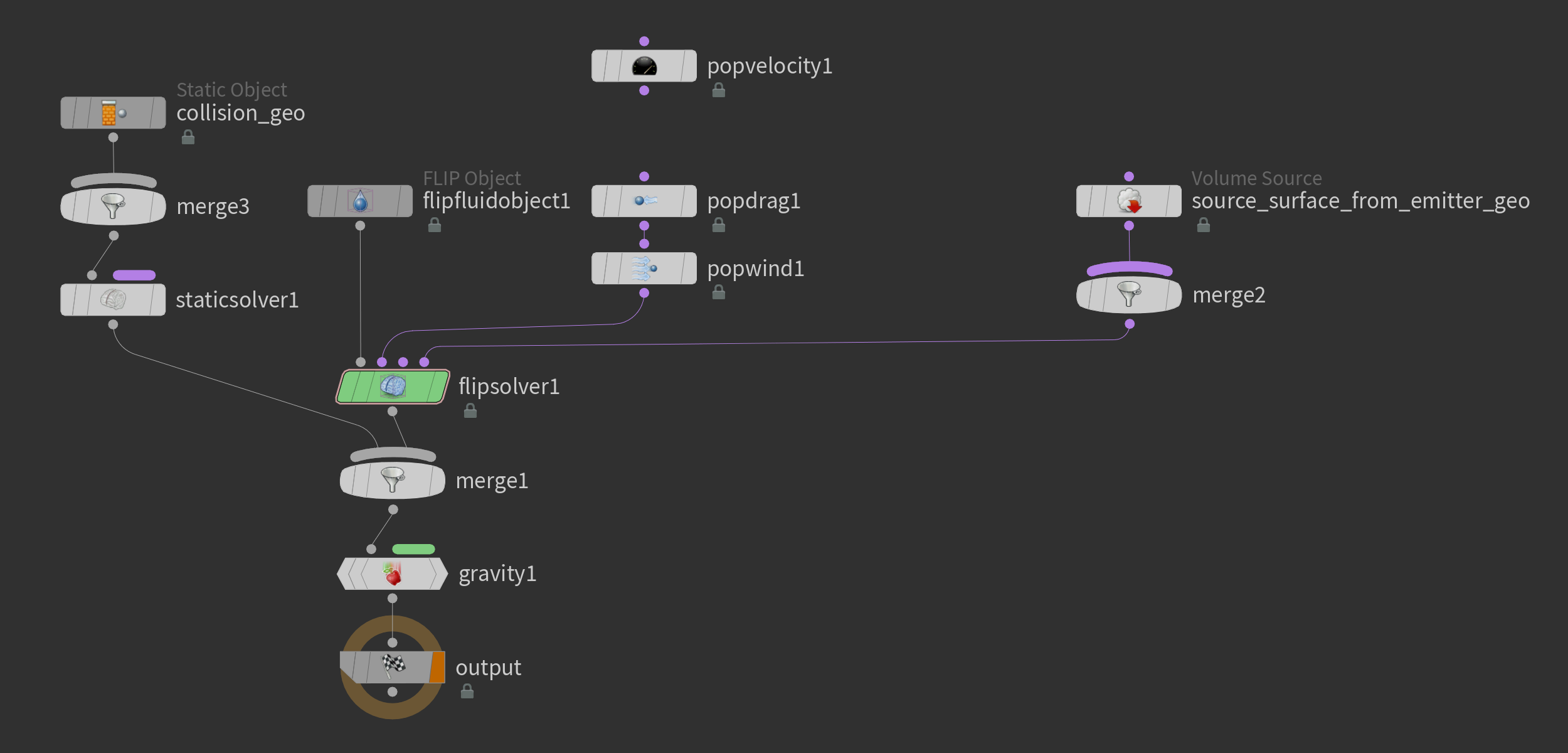
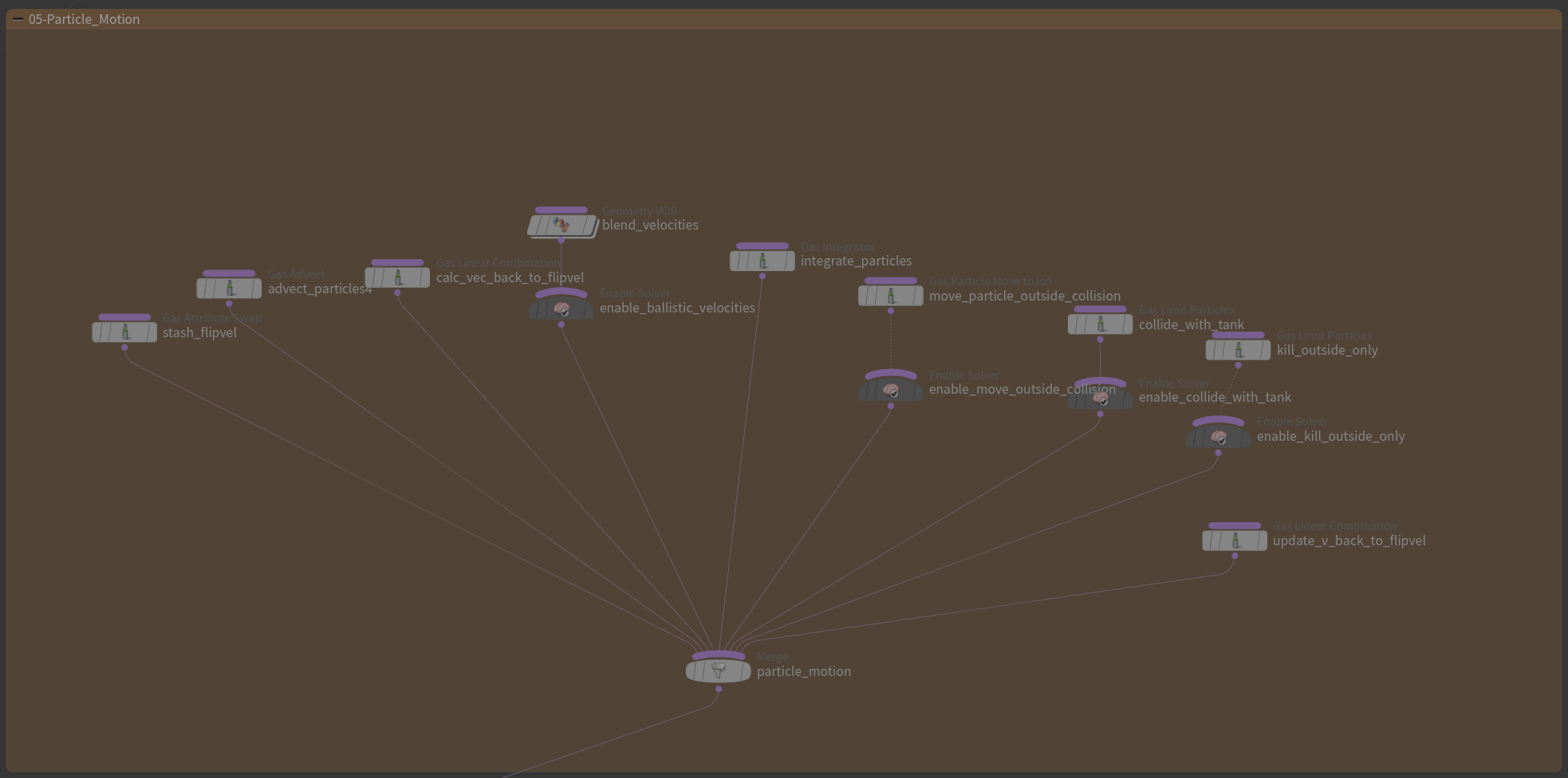
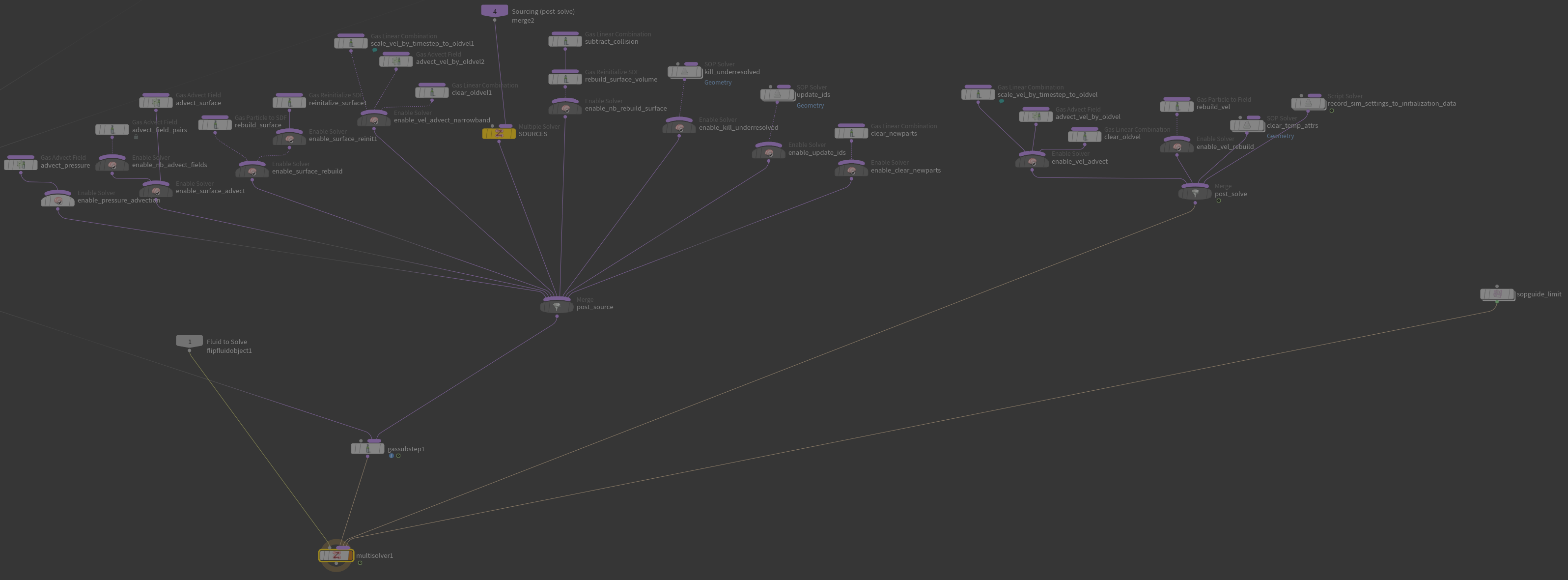
FLIP方法其实只是一个Advection步骤的实现方法，影视工业界通常把结合了FLIP的Advection和Chorin-Style pressure projection，再加上相应需要的粒子网格的工程实现（例如OpenVDB…）的整个流体解算器也称为FLIP——比如我们Houdini工具架上的FLIP模块。我们也利用这个工具制作了一小段流体动画。

在我们的Houdini中，大家可以看到一个完整的FLIP Fluid包括了Geometry的导入、渲染和一个AutoDopNetwork，AutoDopNetwork中是我们的流体解算环节，其中最核心的节点是Filpsolver，大家可以看看这个Flipsolver中，是非常复杂的一个解算结构——但是在学习完前面的所有过程之后，根据每一个部分的名字，我们就逐渐能够看懂了。

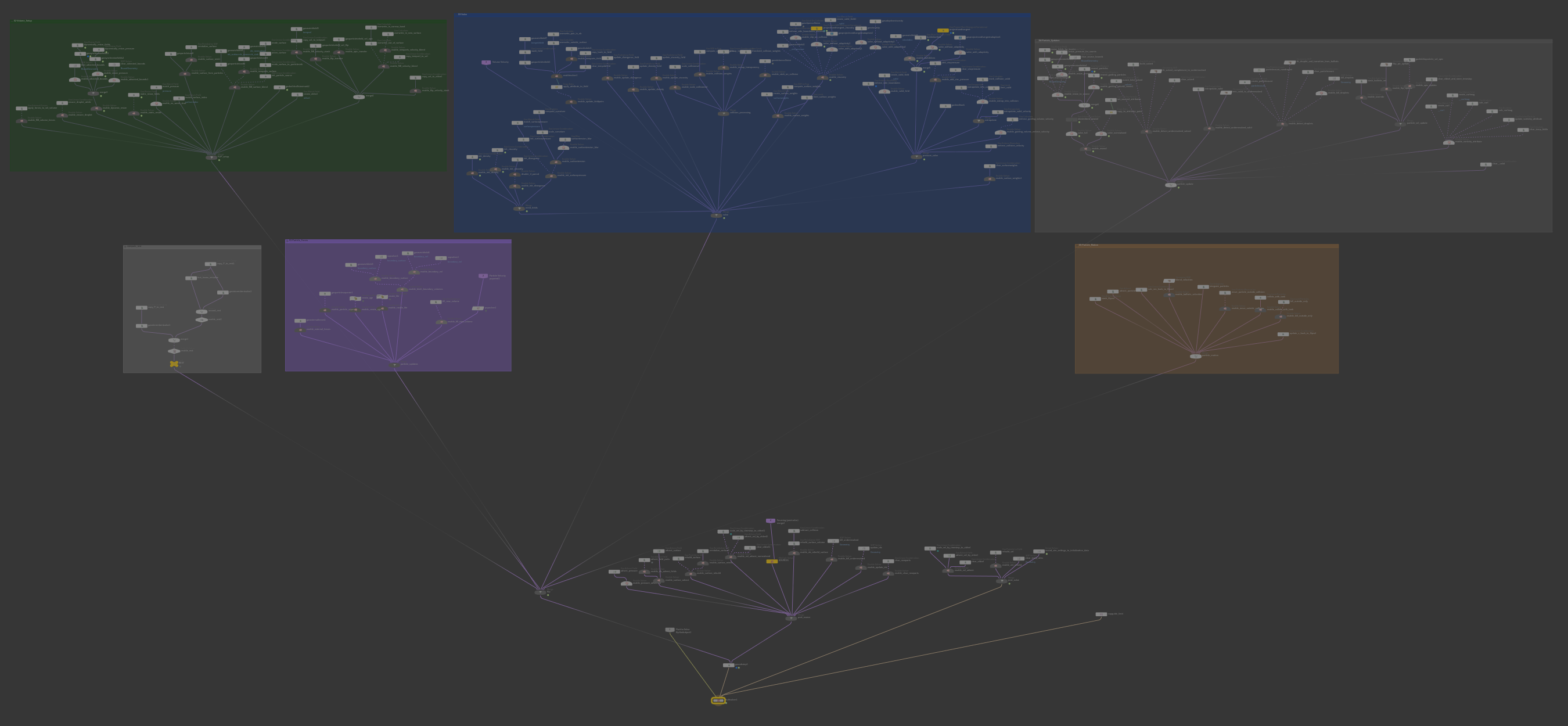
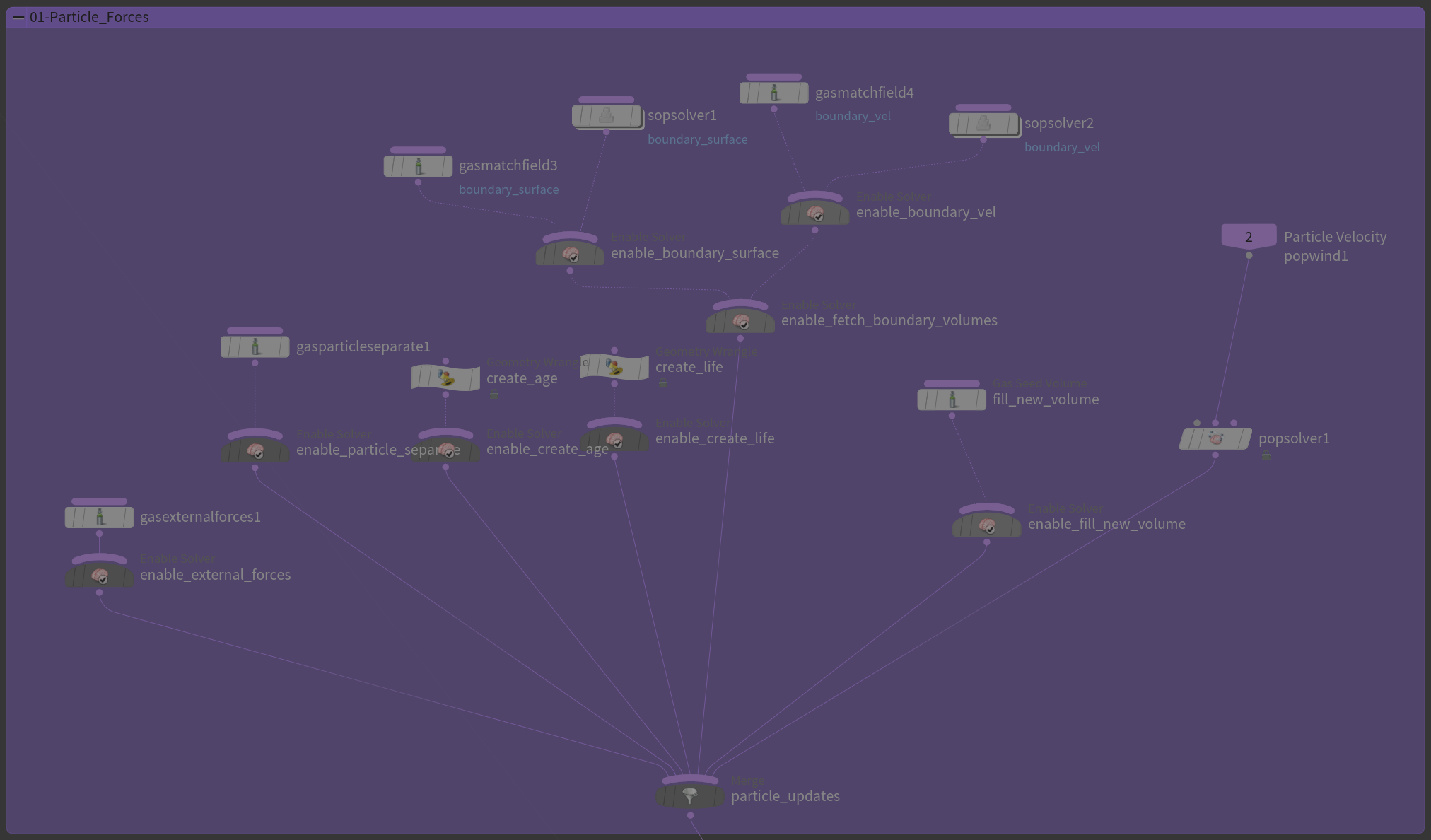
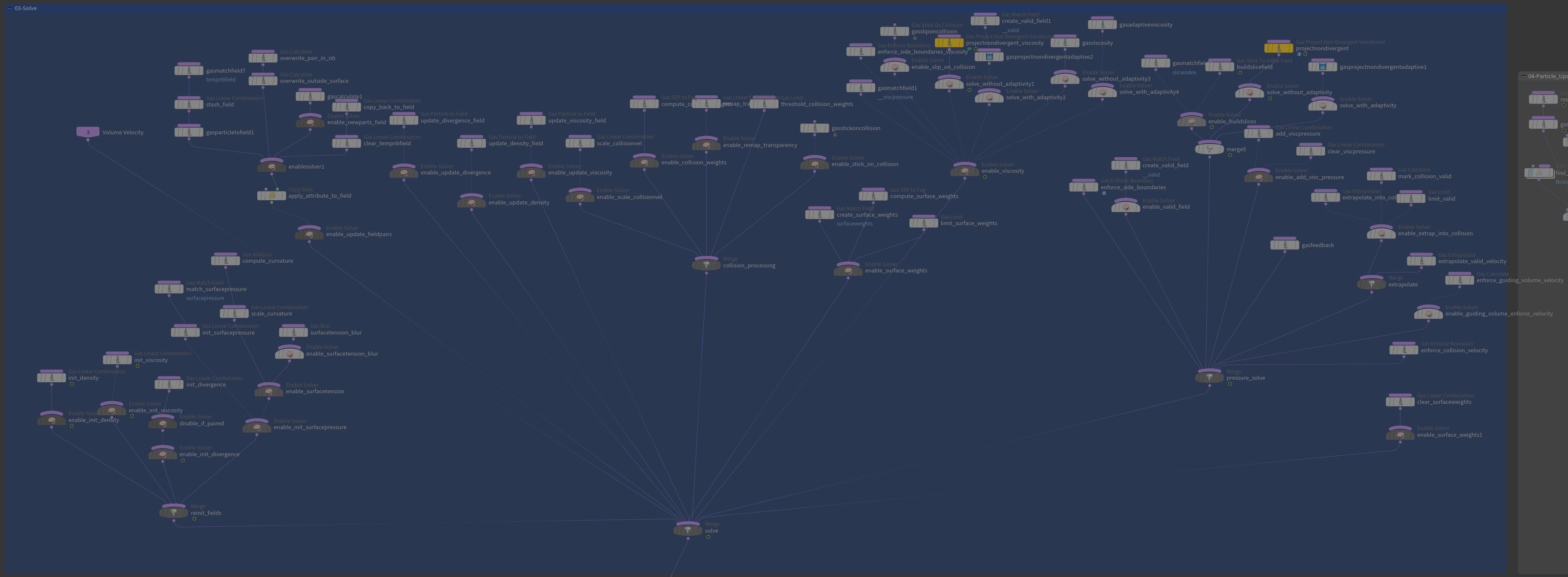
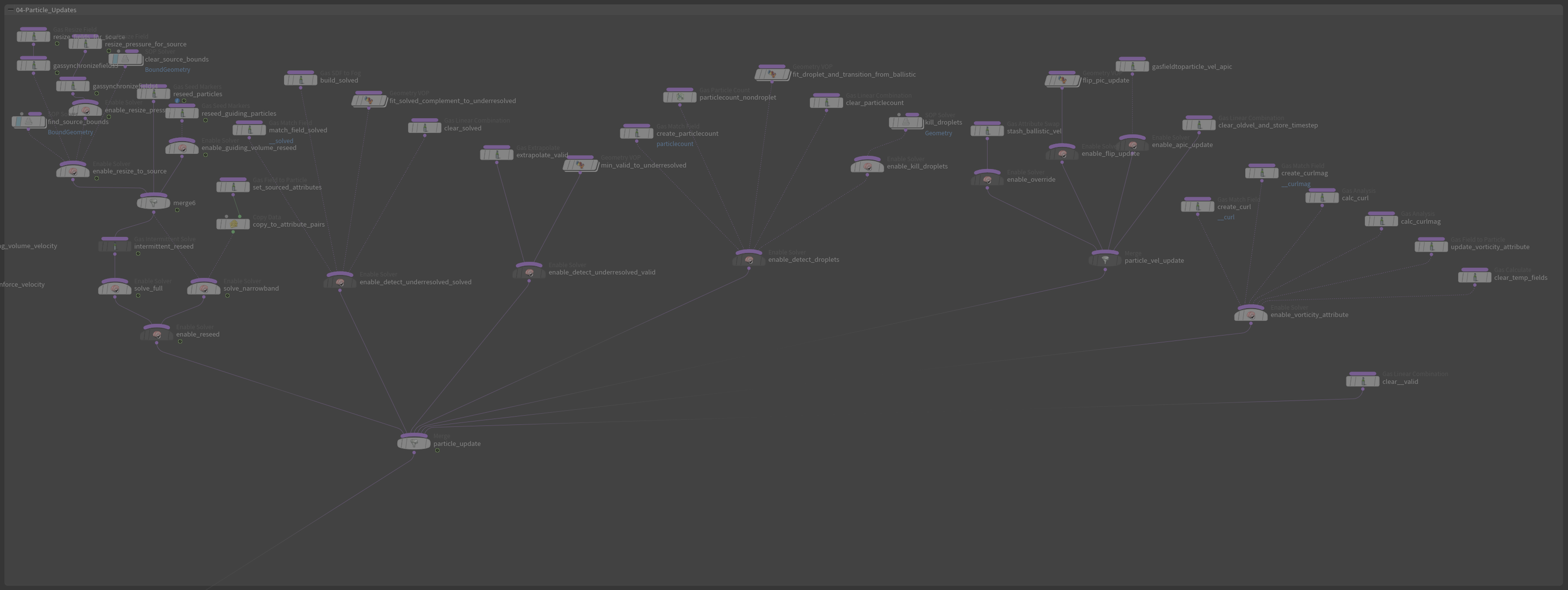
MPM, Material Point Method 物质点法

最后呢，我们来讲一点学术前沿，特别适合用于模拟雪、沙子这种带一点固体性质的流体的方法MPM物质点法[9]，甚至有人拿物质点法去模拟刚体，做我们上一节课介绍的破碎等效果。为什么这样一个流体方法可以用于模拟固体性质呢？

原因在于，我们的粒子域过程中不再只有速度、加速度、受力、温度这些外部属性，而是加入了质量、体积这样的物质属性。而且不再局限于不可压缩流体的Advection和Projection。

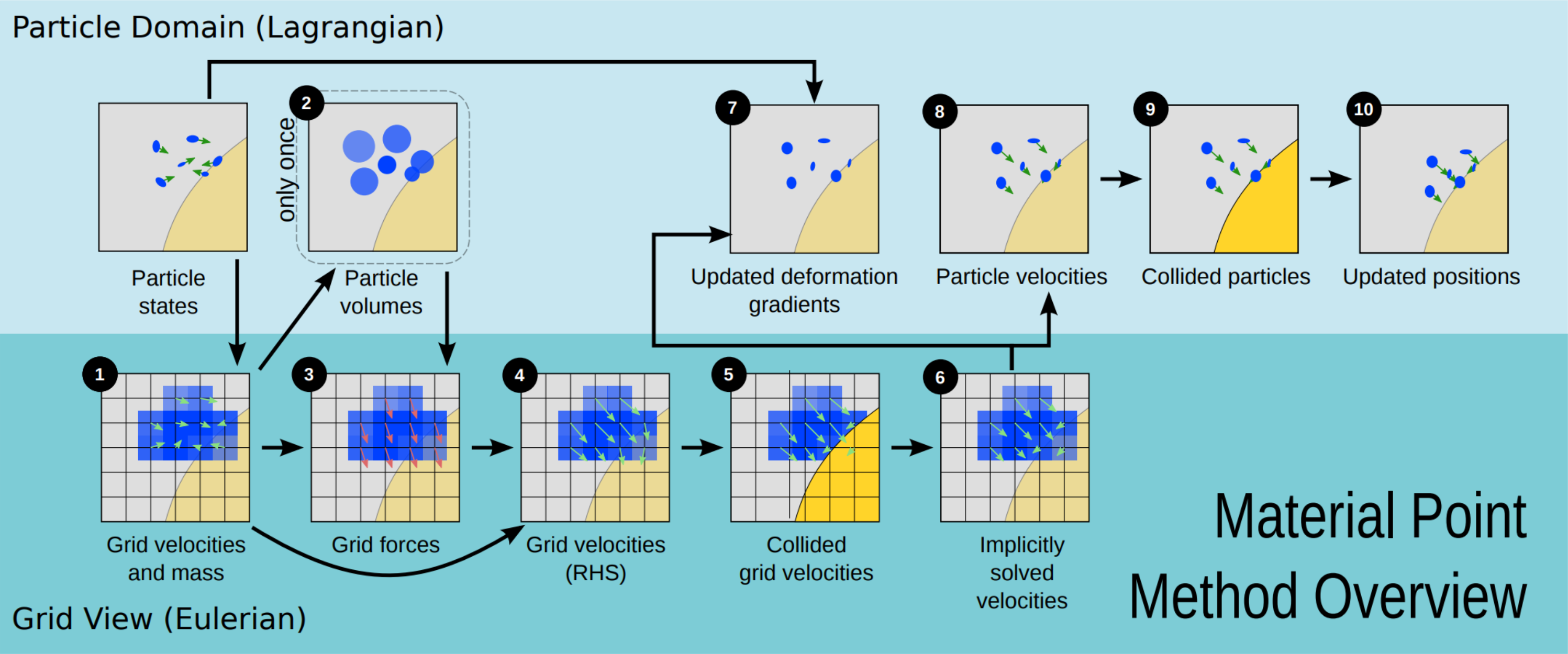
经典MPM方法的流程如下：

1. P2G，传递质量、速度等信息 \(\begin{array}{l}m_i=\sum\nolimits_pm_p\omega_{ip}^n\\\mathbf v_i=\sum\nolimits_p\mathbf v_p^nm_p\omega_{ip}^n/m_i^n\end{array}\)
2. 计算粒子体积和密度 \(\begin{array}{l}\rho_i=m_i^0/h^3\\\rho_p^0=\sum\nolimits_im_i^0\omega_{ip}^0/h^3\\V_p^0=m_p/\rho_p^0\end{array}\)
3. 计算网格受力
4. 更新网格速度场
5. 基于网格的碰撞计算
6. 求解线性方程（迭代法）
7. 更新形变梯度 \(\begin{array}{l}\mathbf F_p^{n+1}=(\mathbf I+\Delta t\nabla\mathbf v_p^{n+1})\mathbf F_p^n\\\nabla\mathbf v_p^{n+1}=\sum\nolimits_i\mathbf v_i^{n+1}(\nabla\omega_{ip}^n)\end{array}\)
8. 更新粒子速度 \(\begin{array}{l}\mathbf v_p^{n+1}=(1-\alpha)\mathbf v_{\mathrm{PIC}p}^{n+1}+\alpha\mathbf v_{\mathrm{FLIP}p}^{n+1}\\\mathbf v_{\mathrm{PIC}p}^{n+1}=\sum\nolimits_i\mathbf v_i^{n+1}\omega_{ip}^n\\\mathbf v_{\mathrm{FLIP}p}^{n+1}=\mathbf v_p^n+\sum\nolimits_i(\mathbf v_i^{n+1}-\mathbf v_i^n)\omega_{ip}^n\end{array}\)
9. 基于粒子的碰撞计算
10. 更新粒子位置 \(\mathbf x_p^{n+1}=x_p^n+\Delta t \mathbf v_p^{n+1}\)

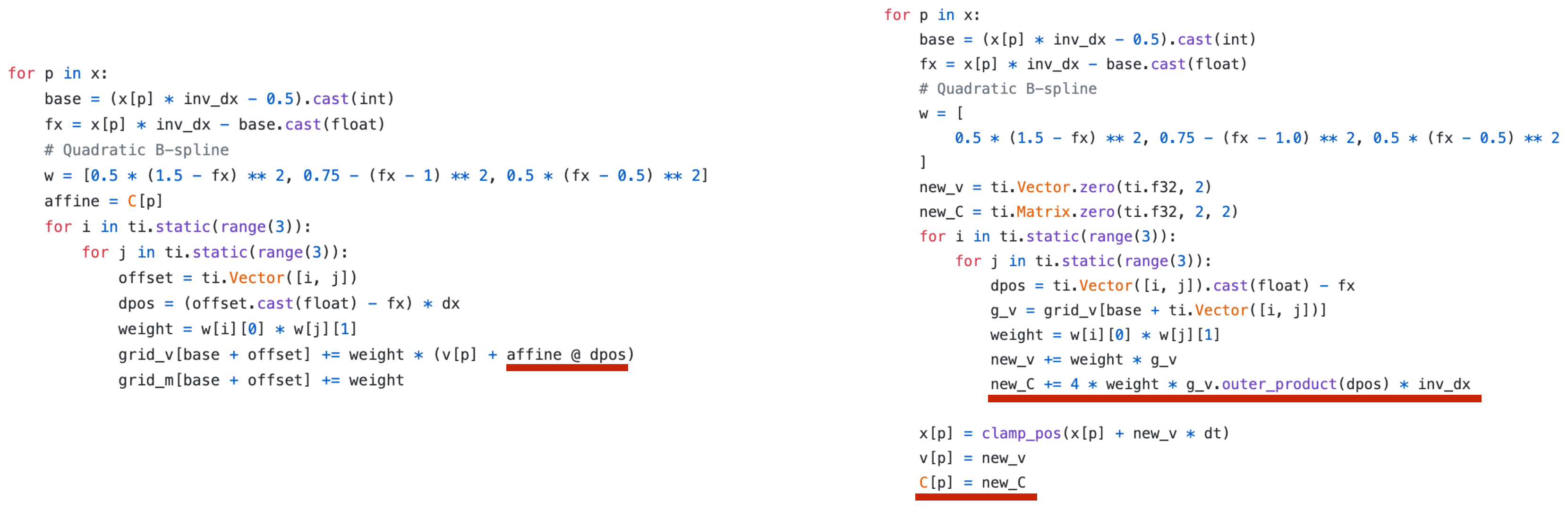
而近年，又有人在APIC的基础上简化了这么复杂的一套MPM方法，提出了MLS-MPM(Moving Least Squares MPM) 移动最小二乘物质点法。

从代码上呈现，就是在前面APIC的代码上，除了Affine分量，还增加一个Stress分量，在更新速度和Affine分量时，利用该Stress分量参与计算，并且需要加上体积的更新。因此实现上相比较经典的MPM方法简单了非常多，也是目前比较流行的一个方法。

这里MPM的数学原理相对复杂了非常多，就不再给大家推导了。

MPM方法非常适合多种材质固体、流体的耦合模拟，处理自碰撞、大形变等等，因此也逐渐在影视工业中投入使用。其中最著名的一个应用案例，就是《冰雪奇缘》中的雪的交互。大家可以欣赏一下影片。当然，发明MLS-MPM的胡渊明博士还有非常火的一篇知乎分享，叫做《99行代码实现〈冰雪奇缘〉》，其实就是MLS-MPM的一个Taichi实现。

案例分析与欣赏

最后还是为大家准备了一些影片中的流体案例。包括《夏日友情天》《寻龙传说》《蜘蛛侠：英雄归来》《沙丘》等。

参考文献 [1] Particle-Based Fluid Simulation for Interactive Applications [2] Smoothed Particle Hydrodynamics Techniques for the Physics Based Simulation of Fluids and Solids [3] Stable fluids [4] Harlow, F.H. (1964) The Particle-in-Cell Computing Method for Fluid Dynamics. Methods in Computational Physics, 3, 319-343. [5] The Affine Particle-In-Cell Method [6] A Polynomial Particle-In-Cell Method [7] FLIP a method for adaptively zoned, particle-in-cell calculations of fluid flows in two dimensions [8] Animating Sand as a Fluid [9] A material point method for snow simulation