Lecture 10-11 Physically-Based Material
Content
- Real-Time Physically-Based Materials
- Microfacet BRDF
- Disney principled BRDF
- Shading with microfacet BRDFs under polygonal lighting
- Linearly Transformed Cosines (LTC)
Concept
- Physically-Based Rendering (PBR)
- Everything in rendering should be physically based
- Materials, lighting, camera, light transport, etc.
- Not just materials, but usually referred to as materials
- PBR materials in RTR
- The RTR community is much behind the offline community
- “PB” in RTR is usually not actually physically based
PBR materials in RTR
For surfaces
- Microfacet models (used wrong so not “PBR”)
- Disney principled BRDFs (artist friendly but still not “PBR”)
For volumes (cloud, hair, skin, etc.)
focused on fast and approximate single scattering and multiple scattering
Recap: Microfacet BRDF
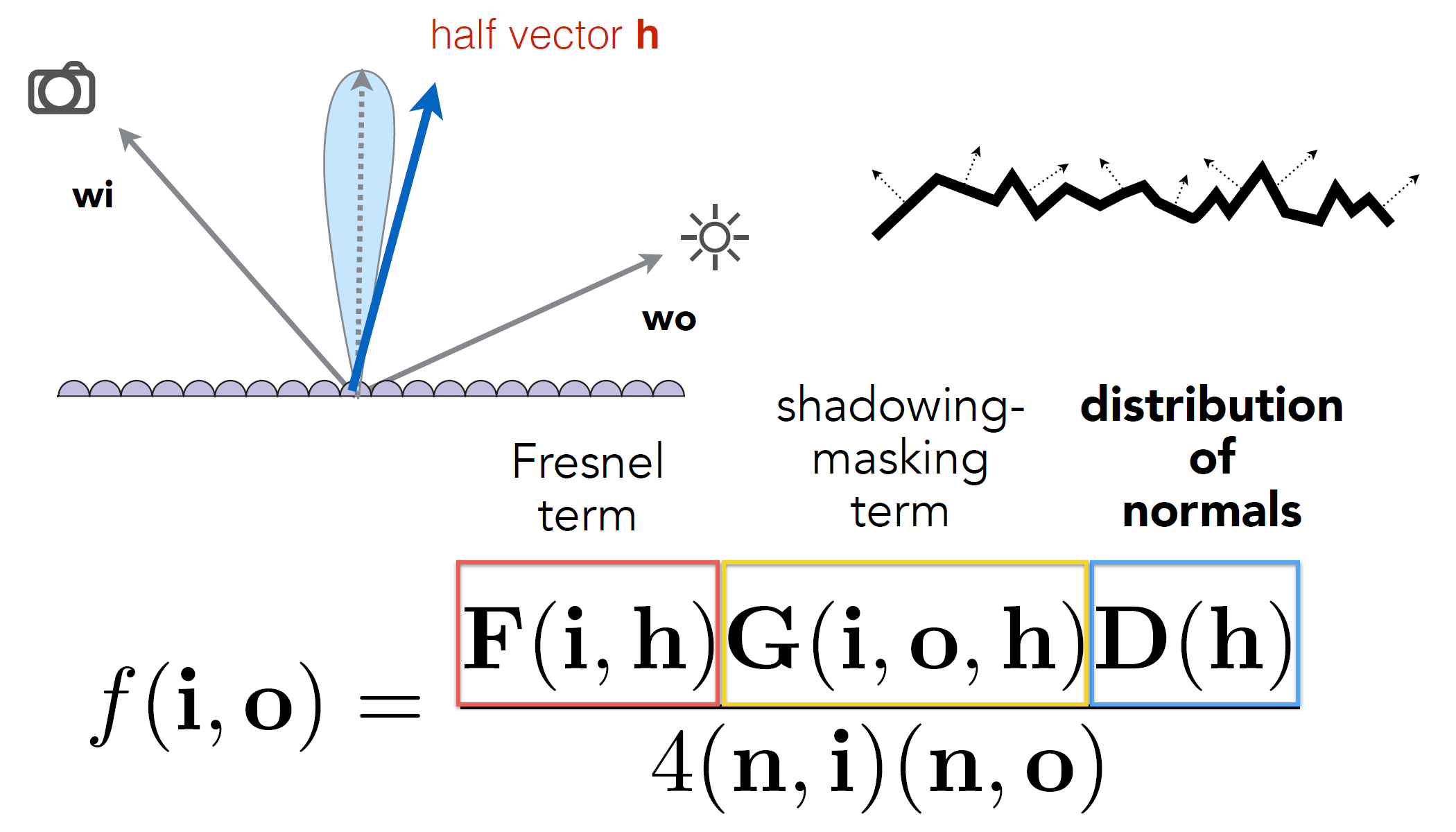
Fresnel term
精确表达非常复杂,需要考虑S/P极化
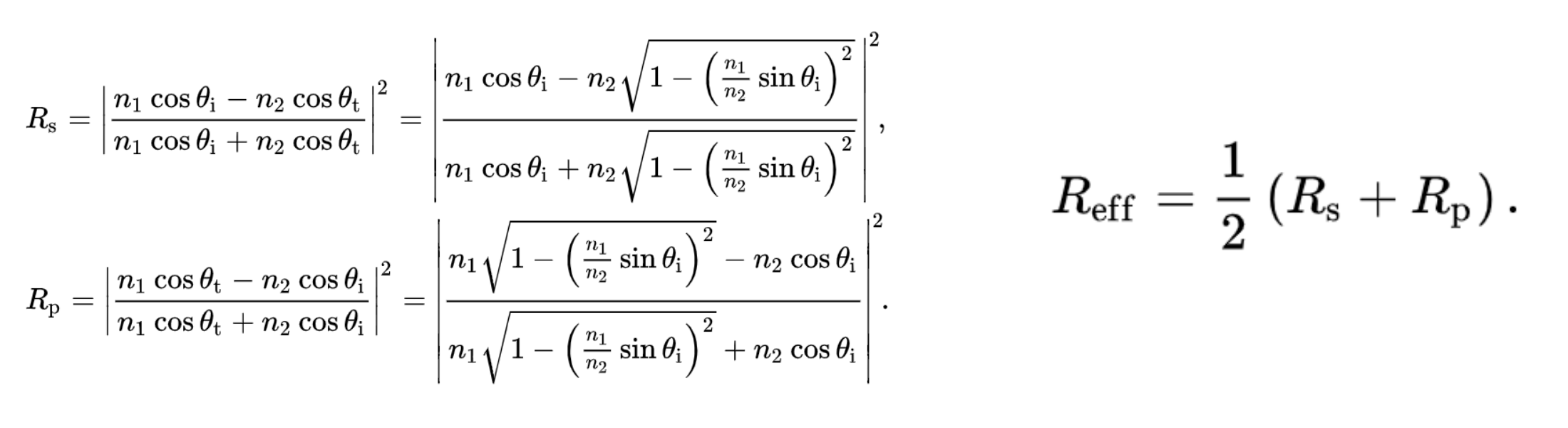
Schlick’s approximation 近似为基础反射率 \(R_0\) 的变化 \[ R(\theta)=R_0+(1-R_0)(1-\cos\theta)^5\\ R_0=\left(\dfrac{n_1-n_2}{n_1+n_2}\right)^2 \]
Normal Distribution Function (NDF)
此处NDF中的Normal为“法线”,须与表示“正态分布”的“Normal Distribution”中的Normal区分
法线分布集中 ==> glossy
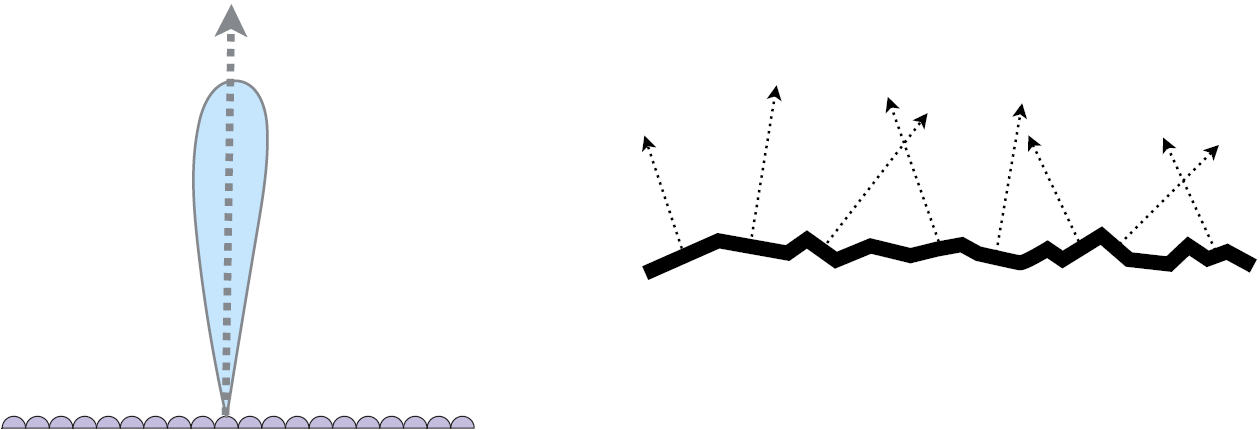
法线分布分散 ==> diffuse
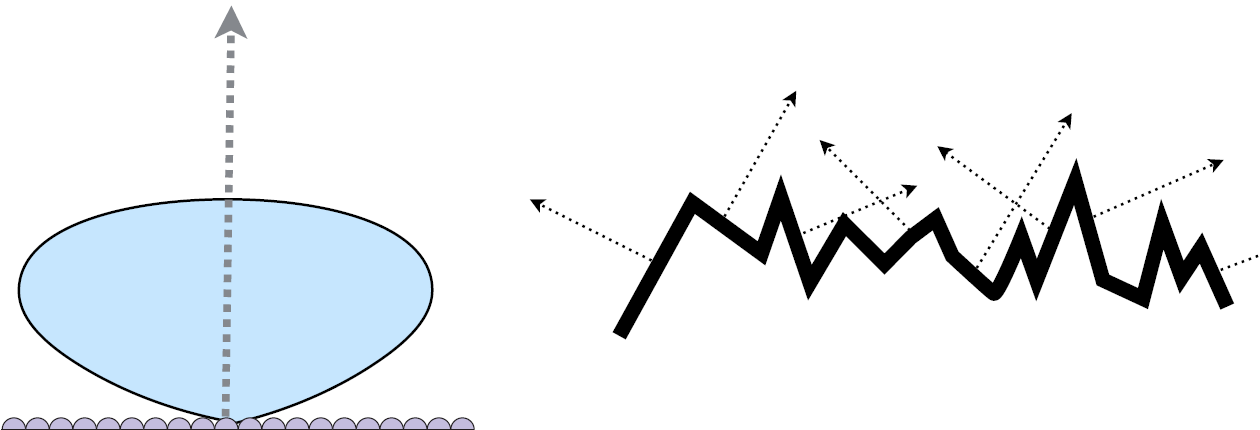
(diffuse的微表面可以视作specular的微表面纵向scale而得到,而纵向scale使得diffuse的微表面“沟壑”较深)
描述NDF的模型
Beckmann NDF \[ D(h)=\dfrac{e^{-\frac{\tan^2\theta_h}{\alpha^2}}}{\pi\alpha^2\cos^4\theta_h}\\ \alpha:\text{roughness of the surface}\\ \theta_h:\text{angle between half vector }h\text{ and normal }n \]
- 类似Gaussian
- 在slope space(坡度空间)上定义 如图即定义在 \(\tan\theta\)
所在平面上(可以保证不出现面朝下的微表面,但较难解决反射光朝下的情况)
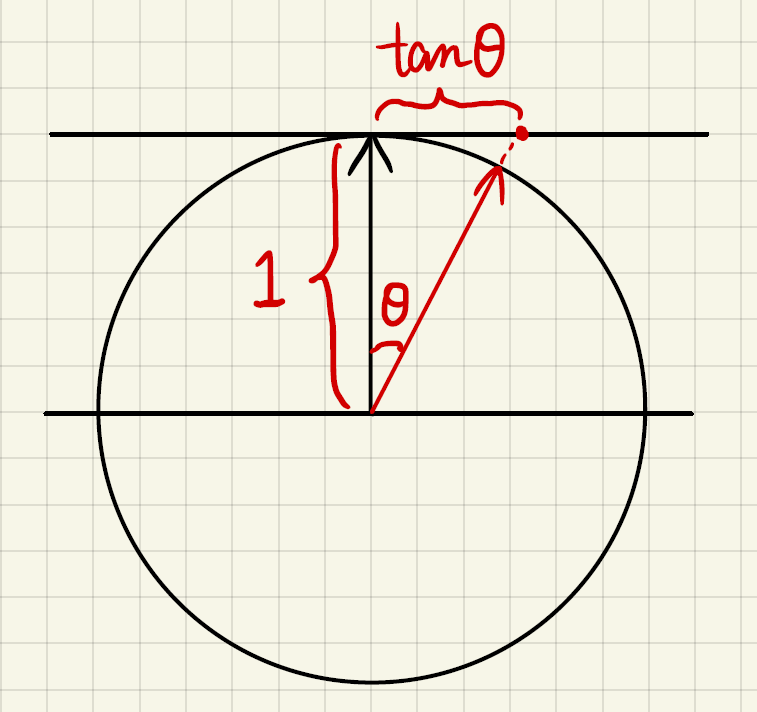
- 在project solid angle上积分为1
GGX (or Trowbridge-Reitz) \[ D_{\rm GGX}(\theta_h) = \frac{\alpha^2}{\pi\cos^4\theta_ m(\alpha^2 + \tan^2\theta_h)^2}\\ \alpha:\text{roughness}^2 \]
- 特征:long tail 长尾巴
衰减到一定程度后非常慢,可使Specular出现“光晕”
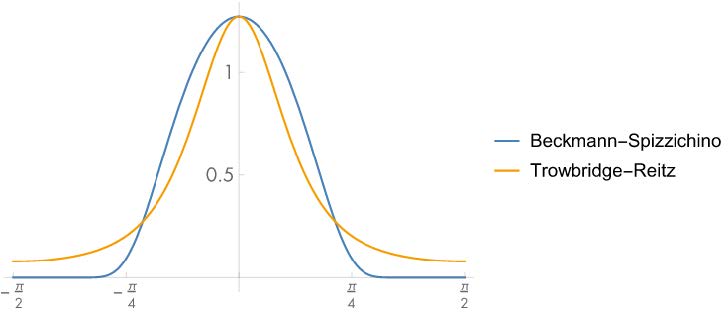
- 对比

- 特征:long tail 长尾巴
衰减到一定程度后非常慢,可使Specular出现“光晕”
Extending GGX
- GTR (Generalized Trowbridge-Reitz) (\(\gamma\)
较大时,接近Beckmann,相当于统一了两种model)
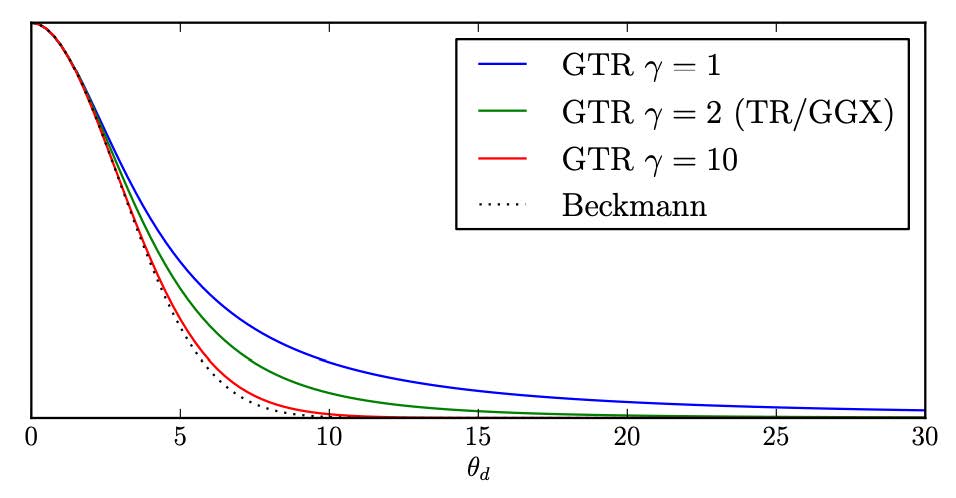
- GTR (Generalized Trowbridge-Reitz) (\(\gamma\)
较大时,接近Beckmann,相当于统一了两种model)
Shadowing-Masking Term
Or Geometry Term : G
解决微表面之间的自遮挡问题
Shadowing 光线照射到微表面
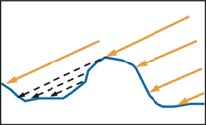
Masking 光线反射进入眼睛
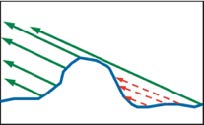
变暗操作,靠近垂直方向时几乎不变暗(G值为1),Grazing angle(掠视)时变暗(G值减小,直至接近0)
常用的Shadowing-Masking Term
Smith Shadowing-Masking Term
把Shadowing和Masking拆开(假定两者无关,事实上有关) \[ G(i,o,m)\approx G_1(i,m)G_1(o,m) \]
Beckmann(绿)和GGX(红)分别的Shadowing-Masking项
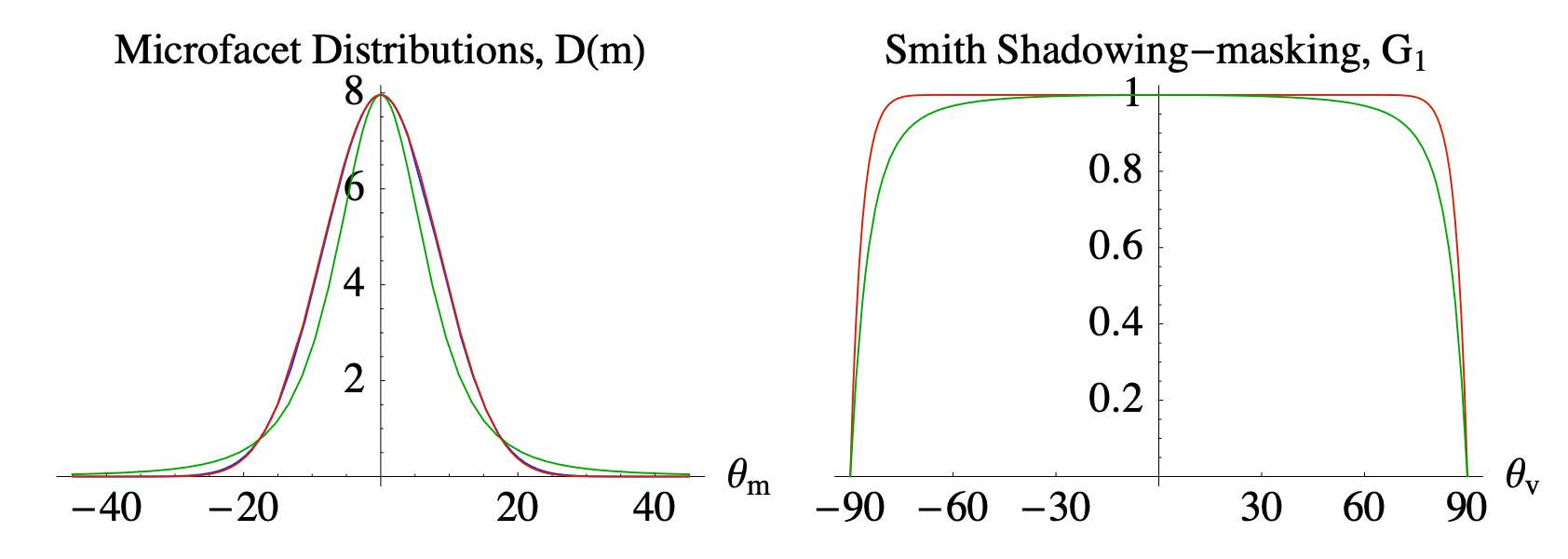
eg. 与GGX法线分布匹配的Smith模型 \[ G_{\rm Smith}(\mathbf{i},\mathbf{o},\mathbf{h})=G_{\rm Schlick}(\mathbf{l},\mathbf{h})G_{\rm Schlick}(\mathbf{v},\mathbf{h})\\ k=\dfrac{({\rm roughness}+1)^2}{8}\\ G_{\rm Schlick}(\mathbf{v},\mathbf{n})=\dfrac{\mathbf{n}\cdot \mathbf{v}}{\mathbf{n}\cdot \mathbf{v}(1-k)+k} \]
问题:能量损失
白炉测试 White Furnace Test:在完全均匀的全局环境光下渲染物体,若物体与背景同色,说明不存在能量损失,若变暗说明存在能量损失。
发现,Roughness值增大会导致能量损失(图2为白炉测试)


Roughness越大,微表面沟壑越多,越容易自遮挡(Shadowing-Masking程度大) ——而现实中,自遮挡的光线经过多次弹射最终会反射出来,不会损失能量,此时Microfacet模型中只考虑了一次弹射
精确地还原损失的能量(Heitz et al. 2016)对实时渲染来说开销过大
Kulla-County Approximation
被遮挡 == 发生下次弹射,从而有该经验性补全多次反射丢失能量的方法
考虑一次反射时有多少能量能够保留:假定入射光 \(L_i=1\) ,BRDF项为 \(f(\mu_o,\mu_i,\phi)\) ,则出射能量(BRDF、cosine、Lighting乘积)的积分为: \[ E(\mu_0)=\int_0^{2\pi}\int_0^1f(\mu_o,\mu_i,\phi)\mu_i\,\mathrm d \mu_i\mathrm d\phi\\\mu=\sin\theta\quad(\text{用}\ \theta,\phi\ \text{定义立体角,换元积分}) \]
则损失能量为 \(1-E(\mu_o)\) ,则只需补上这部分能量
\(E(\mu_o)\) 的积分值与观察方向有关
由于BRDF的可逆性(入射出射互相可逆),则其表示应具有对称性,因此损失能量的形式为: \[ c(1-E(\mu_i))(1-E(\mu_o)) \] (凑积分简化的一种思路)
可得: \[ f_{\rm ms}(\mu_o,\mu_i)=\dfrac{(1-E(\mu_i))(1-E(\mu_o))}{\pi(1-E_{\rm avg})},\quad E_{\rm avg}=2\int_0^1E(\mu)\mu\,\mathrm d \mu \] (推导略)
此时将 \(f_{\rm ms}(\mu_o,\mu_i)\) 作为补全BRDF加入到渲染方程的积分中,就能够补全丢失的能量
总结:设计一个function,即“补充的BRDF”,使得其积分等于丢失能量
问题1: \(E_{\rm avg}=2\int_0^1E(\mu)\mu\,\mathrm d \mu\) 未知且计算困难
- 预计算/打表
- 维度/依赖的参数 —— \(\mu_o\) 和roughness
- 形成一张二维的表在渲染时直接查询
效果

问题2:若BRDF含有颜色
颜色意味着有额外的能量损失(属于应该损失的)
先考虑没有颜色的全局能量损失,求出补全BRDF,再考虑由于颜色造成的能量损失
Average Fresnel:不管入射角大小平均反射的能量占比 \[ F_{\rm avg}=\dfrac{\int_0^1F(\mu)\mu\,\mathrm d\mu}{\int_0^1\mu\,\mathrm d\mu}=2\int_0^1F(\mu)\mu\,\mathrm d\mu \]
\(E_{\rm avg}\) 不参与后续弹射,因此将能量逐步计算
可以直接看到的 \(F_{\rm avg}E_{\rm avg}\)
1次弹射后可以看到 \(F_{\rm avg}(1-E_{\rm avg})\cdot F_{\rm avg}E_{\rm avg}\)
k次弹射后可以看到 \(F_{\rm avg}^k(1-E_{\rm avg})^k\cdot F_{\rm avg}E_{\rm avg}\)
求和求级数得Color Term \(\dfrac{F_{\rm avg}E_{\rm avg}}{1-F_{\rm avg}(1-E_{\rm avg})}\)
将Color Term乘到没有考虑颜色的补全BRDF上,得到最终的补全BRDF,加入渲染方程积分
结果
 ↓
↓

近年出现的不用Kulla-County方法的、不好的Hack: 直接对Microfacet BRDF增加一个diffuse lobe
- eg. 在CV领域作材质识别时
- “完全错误” “不能更糟糕” “我从来没有这么教过你”
- 物理错误,无法保证能量守恒
Shading with Microfacet BRDFs under polygonal lighting – Linearly Transformed Cosines (LTC)
解决微表面模型着色问题
- 主要针对GGX的NDF时(当然其他NDF也可以)
- 不考虑阴影
- 在多边形光源的情况下(不需要采样的方法)
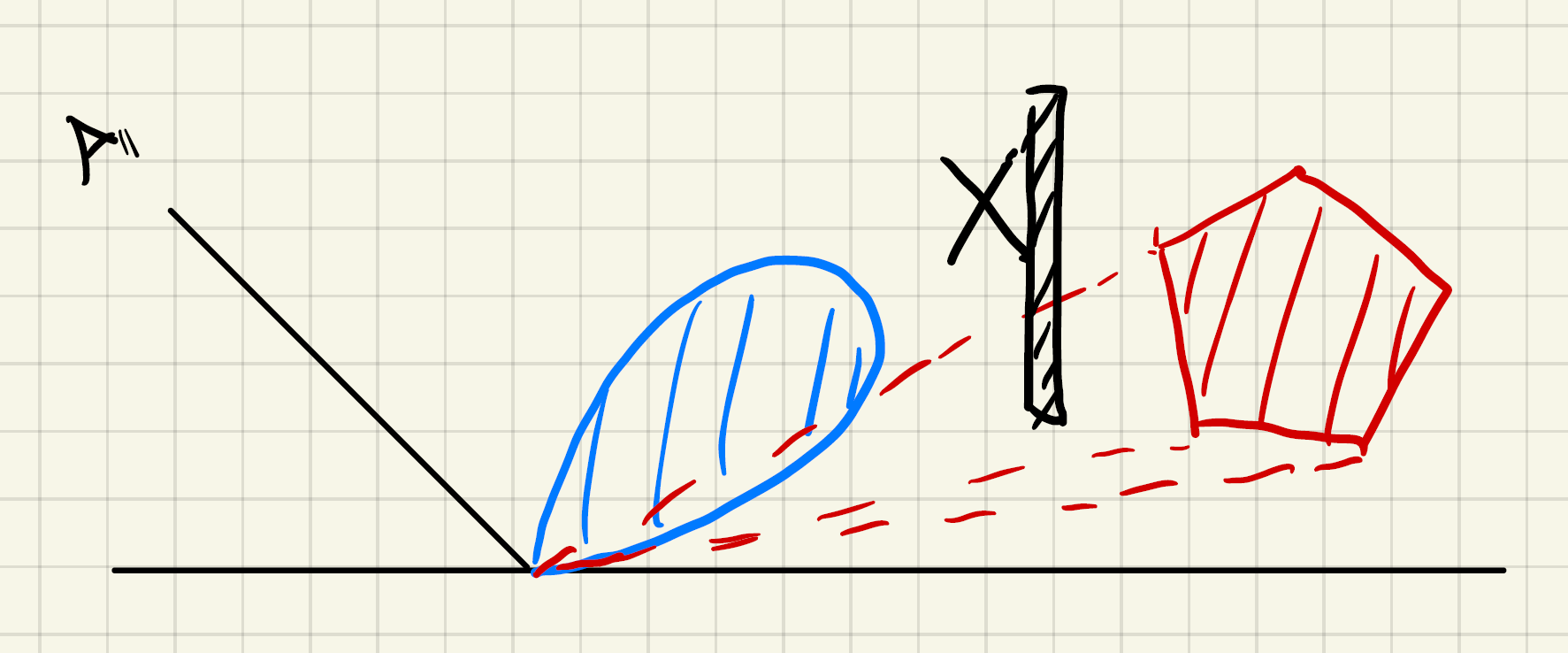
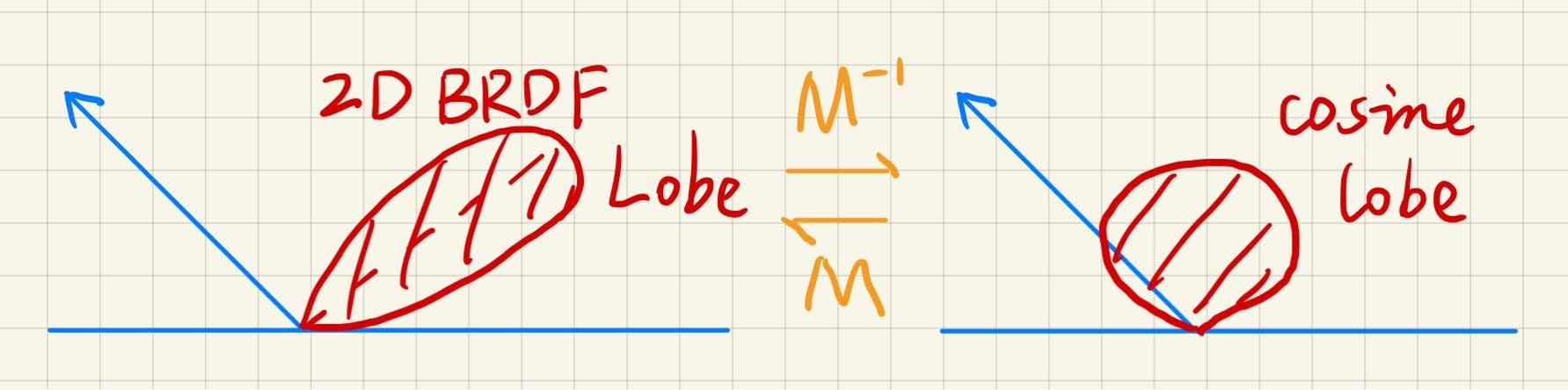
Lobe:瓣,如图蓝色区域,表示从视点发射的光线反射的分布,分布的形状类似一片花瓣。严格定义:BRDF的二维切片(BRDF输入两维、输出两维, \(\theta\) 和 \(\phi\) ,共四维)。
核心想法:
- BRDF的入射/出射的Lobe可以通过线性变换转换成余弦函数(转换到顶部,90度时最大,逐步向外减小)
- 多边形光源也可以作同样的线性变换
- 在这种情况下,在余弦Lobe上积分变形后的光源可以得到解析解
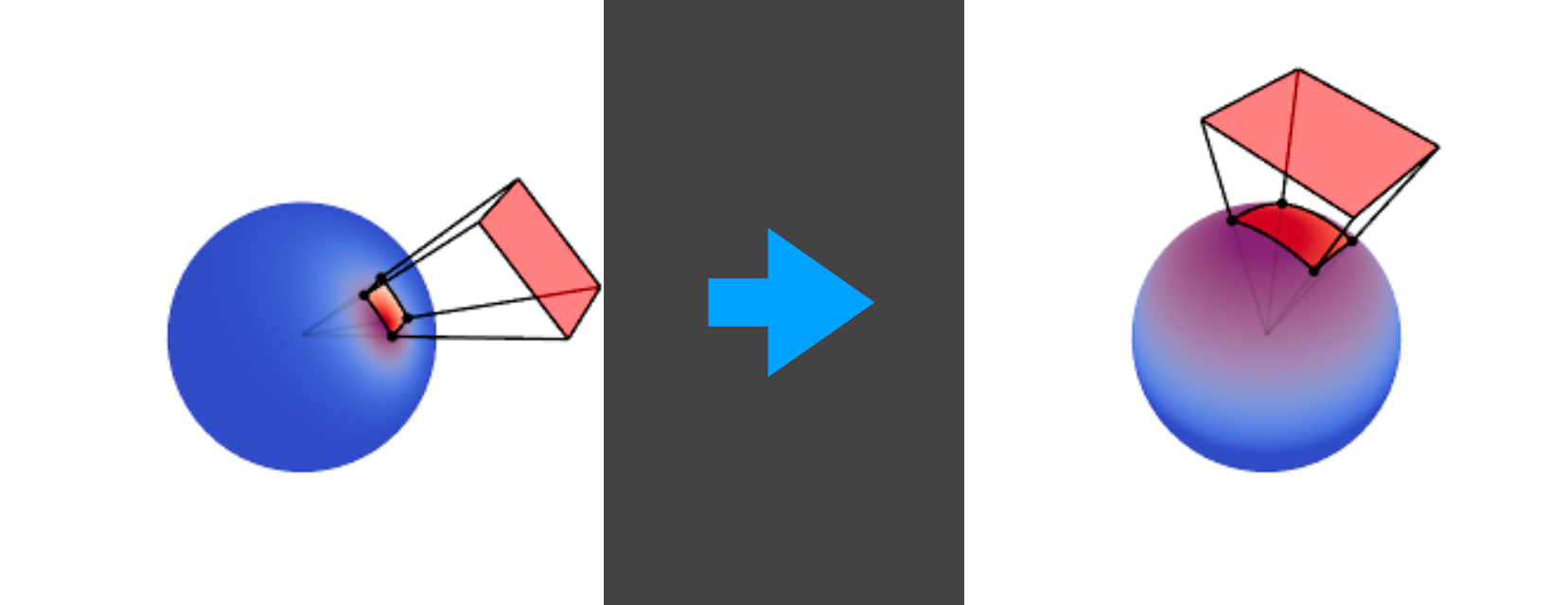
具体做法:
\[ {\rm BRDF}\xrightarrow{M^{-1}}{\rm Cosine}\\ 方向:\omega_i\xrightarrow{M^{-1}}\omega_i'\\ 积分域:P\xrightarrow{M^{-1}}P' \]
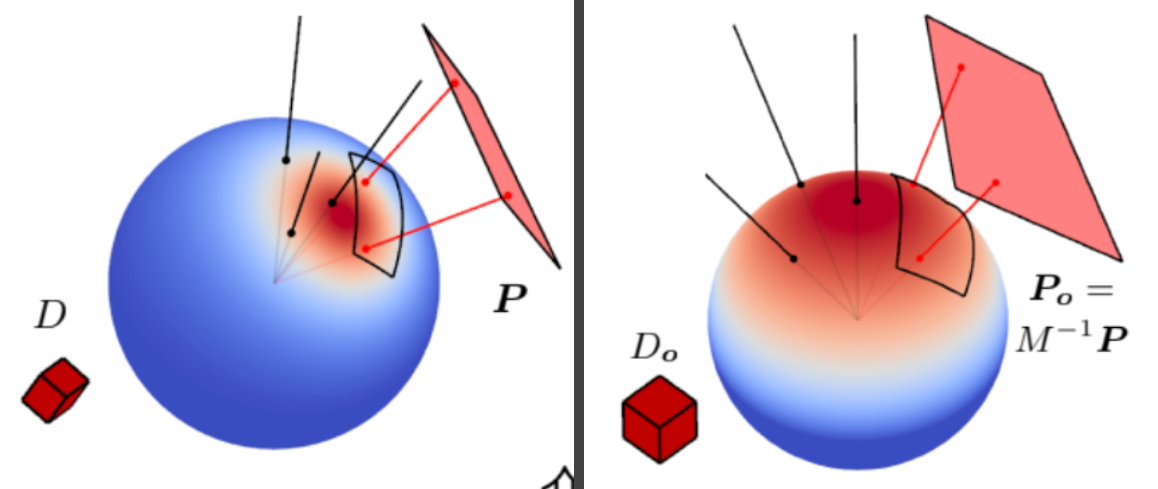
替换一个变量 假设多边形光源是uniform的,即\(L_i\)对各方向保持一致,则 \[ \text{渲染方程}\quad L(\omega_o)=L_i\cdot\int_P F(\omega_i)\,\mathrm d\omega_i\text{(BRDF、Cosine合并为$F()$)}\\ \omega_i=\dfrac{M\omega'_i}{\|M\omega'_i\|}\quad\text{代入替换得}\\ \begin{aligned}L(\omega_o)&=L_i\cdot\int_P\cos(\omega'_i)\,\mathrm d\dfrac{M\omega'_i}{\|M\omega'_i\|}\\&=L_i\cdot\int_{P'}\cos(\omega'_i)J\,\mathrm d\omega'_i\end{aligned} \]
如何得到\(M\):预计算(给初始值通过优化方法计算)
Disney Principled BRDF
为什么需要?
- Microfacet模型不能表征所有真实感材质
- 不够Diffuse
- 无法解释多层材质(eg.刷有清漆的表面)
- Microfacet模型不够Artist-friendly
- eg. 定义折射率的\(n\)和\(k\)
Disney Principled BRDF设计原则
- Art directable,不必须物理真实
- 还是一定程度上基于物理的(在实时渲染中)
Principle 原则
- 看起来直观,不用物理量
- 尽可能减少参数
- 0-1范围
- 允许<0和>1情况,呈现特殊效果
- 具有稳健性
Disney Principled BRDF建立在拟合的基础上,有开放源码
sheen : 绒毛,在grazing angle上有类似羽化效果 clearcoat : 类似清漆的透明层
维度多时,会出现多种参数呈现类似结果的现象
优劣势
- 易于理解/控制
- 能描述的材质广泛
- 开源的实现
- 不完全基于物理
- 巨大的参数空间
Non-Photorealistic Rendering
== (fast and reliable) stylization
风格化
- 描边
- 模型简化、色块
- 阴影分界线
轮廓
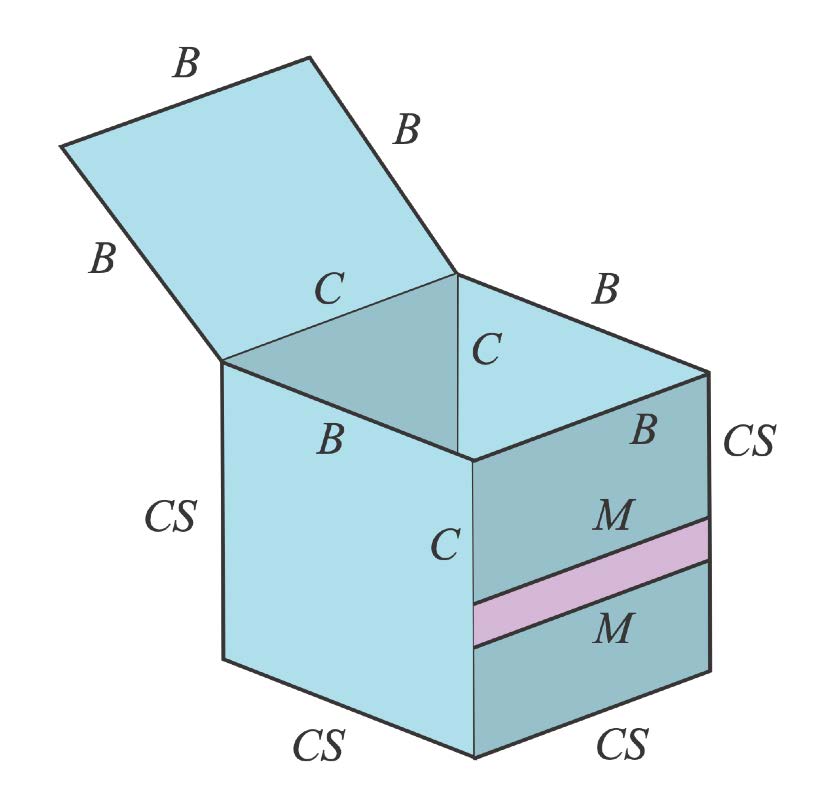
分类
- 边界 Boundary / Border edge
- 折痕 Crease
- 材质边缘 Material edge
- 有多个面共享的外轮廓线 Silhouette edge
Silhouette edge 描边绘制
Silhouette edge处观察方向与法线方向几乎垂直
- 设定观察方向与发现夹角的阈值,超过的像素设黑
- 问题:描边粗细不一样
背面的三角形/模型扩大一小圈渲染为黑
图像后处理:Edge Detect
Sobel Detector 纵向/横向,色块处两侧抵消,分界线两侧不抵消 \[ \begin{bmatrix} 1 & 0 & -1\\ 2 & 0 & -2\\ 1 & 0 & -1 \end{bmatrix}\quad \begin{bmatrix} -1 & -2 & -1\\ 0 & 0 & 0\\ 1 & 2 & 1 \end{bmatrix} \]


利用G-Buffer信息,深度、法线等
色块
- 先得到正常的shading结果,再做一个阈值化(多值化 Quantization)
- 在不同的部分(Diffuse、Specular…)应用不同的阈值化方法
素描效果
- 阴影部分打横竖线格,格子密度与阴影明暗相关
- 提前设计不同密度的格状纹理查询(结果邻近像素查询纹理邻近像素,保证笔触连续)
- 对每种纹理做MIPMAP时,保证每一级MIPMAP的密度一致(类似裁切而非等比缩小)

真实感模型是非真实感渲染的基础。