Lecture 5-6 Environment Lighting

Recap

  • 环境光贴图
  • 球面贴图 Spherical Map / 立方体贴图 Cube Map

Shading from Environment Lighting / Image-Based Lighting (IBL)

  • 解渲染方程（不考虑阴影） \[ L_o(\mathrm p,\omega_o)=\int_{\Omega^+}L_i(\mathrm p,\omega_i)f_r(\mathrm p,\omega_i,\omega_o)\cos\theta_i\xcancel{V(\mathrm p,\omega_i)}\,\mathrm d\omega_i \]

    • 蒙特卡洛积分——数值解、大量采样，非常慢 PS: 一旦涉及采样，就很难实时，近年开始有一些进展

  • 观察：

    • glossy BRDF : BRDF覆盖很小
    • diffuse BRDF : BRDF覆盖大，但是平滑

    IBL1

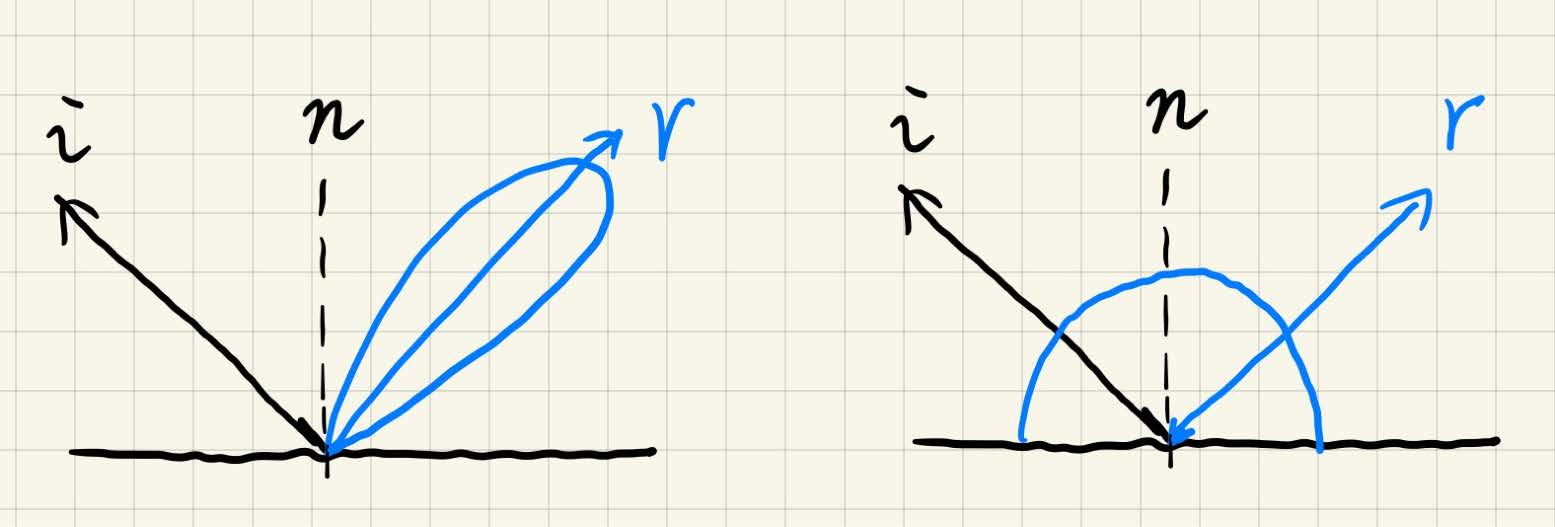
  • 因此考虑近似方法 \[ \int_\Omega f(x)g(x)\,\mathrm dx\approx\dfrac{\int_{\Omega_G}f(x)\,\mathrm dx}{\int_{\Omega_G}\,\mathrm d x}\cdot\int_\Omega g(x)\,\mathrm dx \] （该式在 \(g(x)\) 范围小/结果平滑时较为准确）

    则有 \[ L_o(\mathrm p,\omega_o)\approx\dfrac{\int_{\Omega_{f_r}}L_i(\mathrm p,\omega_i)\,\mathrm d\omega_i}{\int_{\Omega_{f_r}}\,\mathrm d\omega_i}\int_{\Omega^+}f_r(\mathrm p,\omega_i,\omega_o)\cos\theta_i\,\mathrm d\omega_i \]

  • \(\dfrac{\int_{\Omega_{f_r}}L_i(\mathrm p,\omega_i)\,\mathrm d\omega_i}{\int_{\Omega_{f_r}}\,\mathrm d\omega_i}\) 表示对环境光贴图做模糊化处理，即滤波

    • Prefiltering：在渲染之前就做好滤波
    • 多种大小滤波核的结果，类似MIPMAP，计算时再做查询插值 【积分某区域的结果 = 先做区域的求和再取值】

    IBL2

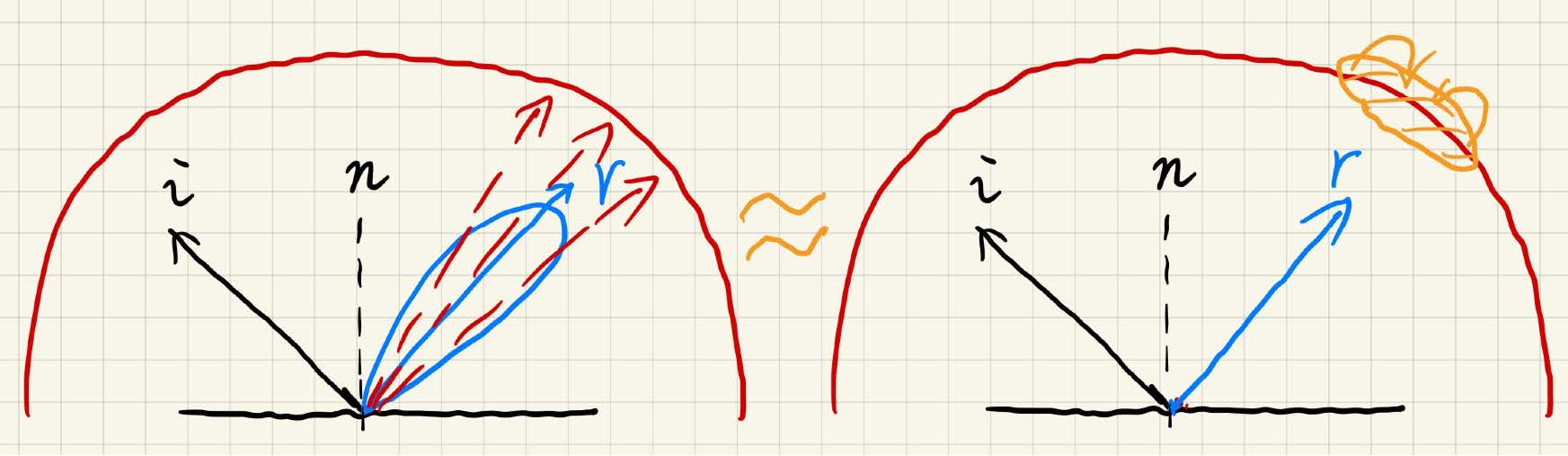
  • \(\int_{\Omega^+}f_r(\mathrm p,\omega_i,\omega_o)\cos\theta_i\,\mathrm d\omega_i\) 部分则做预计算

    • eg. Microfacet BRDF : Fresnel + NDF + Shadowing-Masking 需要一个巨大的表（至少五维参数）

    • Fresnel : Schlick’s approximation \[ R(\theta)=R_0+(1-R_0)(1-\cos\theta)^5\\ R_0=\left(\dfrac{n_1-n_2}{n_1+n_2}\right)^2 \]

    • NDF : eg. Beckmann distribution \[ D(h)=\dfrac{e^{-\frac{\tan^2\theta_h}{\alpha^2}}}{\pi\alpha^2\cos^4\theta_h}\quad\text{$\alpha$:Roughness} \]

    • 将半程向量与入射出射光夹角、法线与入射出射光夹角、入射出射光夹角的一半都近似认为是 \(\theta\) ，则减少至三维参数表

    • 将Fresnel项写在原式中作近似： \[ \begin{aligned}&\int_{\Omega^+}f_r(\mathrm p,\omega_i,\omega_o)\cos\theta_i\,\mathrm d\omega_i\\ \approx& R_0\int_{\Omega^+}\dfrac{f_r}{F}(1-(1-\cos\theta_i)^5)\cos\theta_i\,\mathrm d\omega_i\\ +&\int_{\Omega^+}\dfrac{f_r}{F}(1-\cos\theta_i)^5\cos\theta_i\,\mathrm d\omega_i\end{aligned} \] 将基础反射率 \(R_0\) （Base Color）解放出来 -> 二维参数表

    • 二维参数表：\(\text{Roughness}(\alpha) - \cos\theta\) IBL3

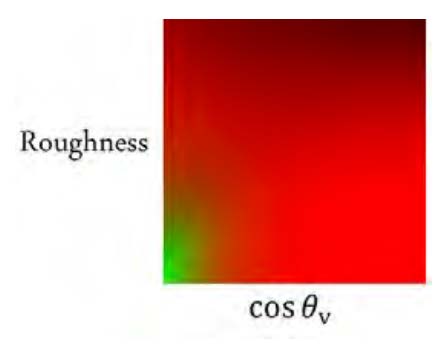
  • 这一方法称为 Split Sum （积分 -> 求和）

Precomputed Radiance Transfer, PRT

实时渲染中很难做到环境光下的阴影

  • 把环境光看作大量光源：需要大量的shadow map
  • 把问题看成一个采样问题：有不同的遮挡情况、不同的Visibility，Visibility项也不能用近似方法分离出来
  • 一个解决思路：从最亮的光源下生成阴影（例如太阳）
  • 相关工作
    • Imperfect shadow maps
    • Light cuts
    • RTRT (might be the Ultimate Solution)
    • PRT
Spherical Harmonics, SH 球面谐波函数
  • 傅里叶级数：把一个函数拆成无数sin/cos函数（基函数）之和
  • Filtering 滤波
  • 形如 \(\int_{\Omega}f(x)g(x)\,\mathrm dx\) 可以视作滤波操作
    • 低频信息 == 平滑的函数
    • 积分后频率是两个相乘的函数中较低的那个
  • 基函数：\(f(x)=\sum_ic_i\cdot B_i(x)\) ，则 \(B_i(x)\) 称基函数

SH：定义在球面上的一系列二维的基函数（理解为关于方向的函数，球面上的方向用 \(\theta\,\phi\) 描述）

  • 很像一维的傅里叶级数 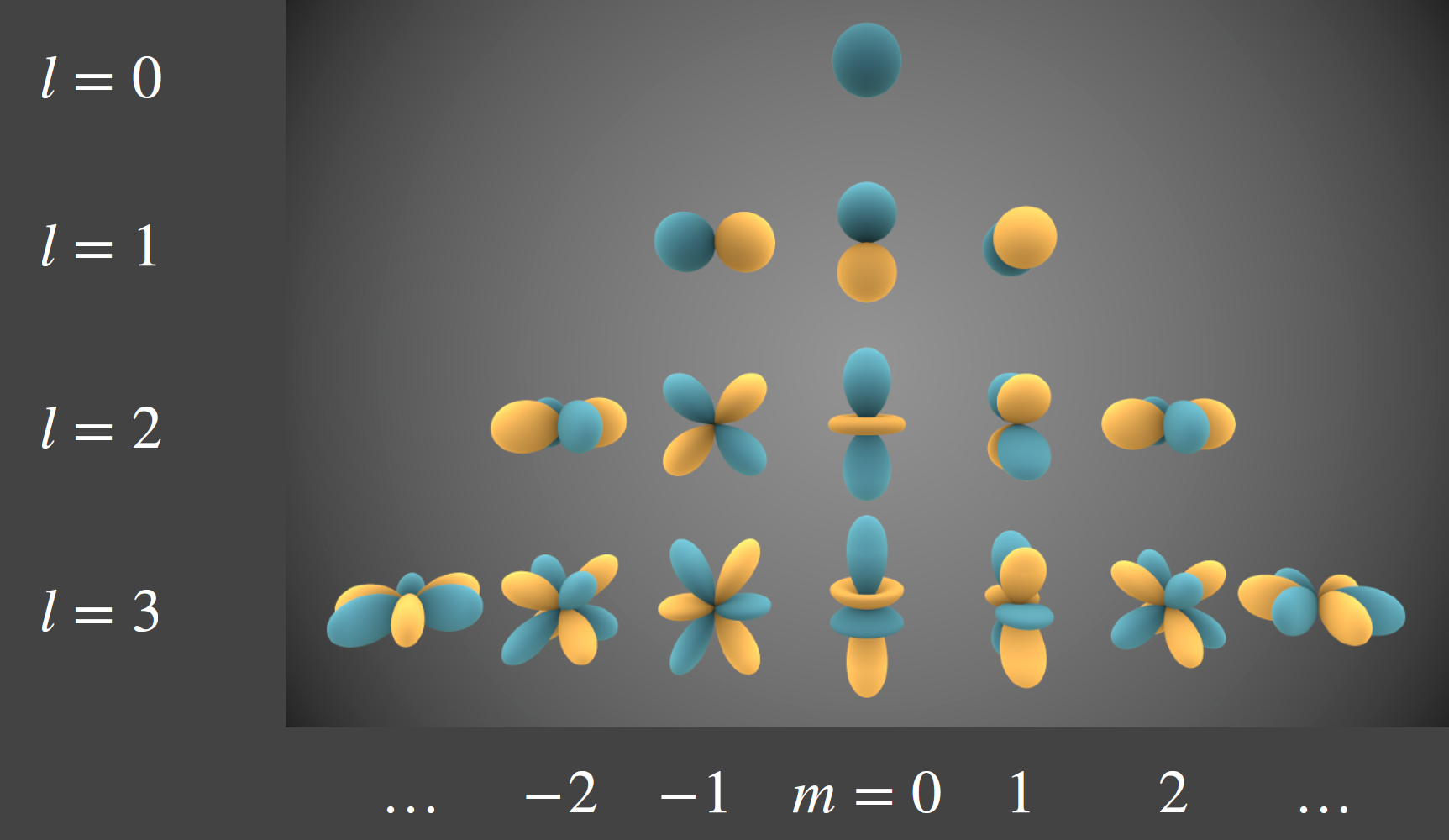SH1 （颜色深度表示值，黄蓝表示正负？；l：阶数）

  • SH的基函数，用勒让德多项式表示（这里不必写出公式）

  • 用基函数 \(B_i(\omega)\) 的线性组合，即可表示二维函数

  • 基函数 \(B_i(\omega)\) 的系数用 \(f(\omega)\) 表示，则有 \[ c_i=\int_\Omega f(\omega)B_i(\omega)\,\mathrm d\omega \] （求系数的过程数学上称为“投影”）

  • 用前 \(n\) 阶系数可恢复出近似的原函数， \(n\) 越大，保留系数越多

对Diffuse材质应用SH

  • Recall : Prefiltering of Envirnment Light Prefiltering + single query == No filtering + Multiple queries

  • Diffuse BRDF 很像低通滤波器（光照与BRDF做逐点相乘再积分，即Product Integrate）

    考虑用少量SH来描述Diffuse BRDF（例如前3阶）

  • 高频函数与低频函数Product Integrate，频率由低频函数决定 -> 既然Diffuse BRDF是低频的，那么光照也无需记录高频

    考虑也用SH来描述来描述光照（例如前3阶）

  • 非常简单的实现

    surface float1 irradmat(matrix4 M, float3 v) {
  float4 n = {v, 1};
    return dot(n, M*n);
}
解决阴影、不限制Diffuse的方法：PRT

\[ L_o(\mathrm p,\omega_o)=\int_{\Omega^+}L_i(\mathrm p,\omega_i)V(\mathrm p,\omega_i)f_r(\mathrm p,\omega_i,\omega_o)\cos\theta_i\,\mathrm d\omega_i \]

  • Light、Visibility、BRDF三项均描述成球面函数

  • eg. 用Cubemap存时，每个shading point的计算量过大

  • 考虑用SH来预计算部分内容

    • 认为Light在场景中可变；Visibility、BRDF等无关项认为是Light Transport，不可变
    • Light：用SH近似 \(L_i\approx\sum l_iB_i\)
    • Light Transport：渲染之前做预计算

  • Diffuse情况 PRT1

    • 运行时则只需要算点乘

    • 但是Visibility项固定意味着场景不能动

    • Light：光源本身旋转不可用（后面会说可以计算）

    • 重新理解

      • Light : \(L(\omega_i)\approx\sum_pc_pB_p(\omega_i)\) Light Transport : \(T(\omega_i)\approx\sum_qc_qB_q(\omega_i)\)
      • 则渲染方程 \[ L_o(\mathrm p,\omega_o)=\sum_p\sum_qc_pc_q\int_{\Omega^+}B_p(\omega_i)B_q(\omega_i)\,\mathrm d\omega_i \] 由于SH基函数正交，则仅当 \(p=q\) 时，右边积分结果有意义，否则为零。复杂度 \(O(n^2)\) 降低至 \(O(n)\) 。

  • SH的性质

    • 基函数相互正交
    • 易于计算投影（函数与任一基函数做Product Integrate即可）
    • 易于计算旋转
      • 相当于旋转每一个SH基函数
      • SH基函数的旋转可以用同阶基函数的线性组合表示
      • 打表格
    • 易于卷积
    • 少量基函数代表低频

  • 把多次Bounce的过程也视作Light Transport，预计算，可实现GI

  • Glossy情况

    • Light Transport 包含Visibility和BRDF，对于给定的出射方向 \(\mathrm o\) ，BRDF都不一样 -> \(T_i(\mathrm o)\)

    • \[ T_i(\mathbf o)=\sum t_{ij}B_j(\mathbf o)\\ L_o\approx\sum l_iT_i(\mathbf o)\approx\sum\left(\sum l_i t_{ij}\right)B_j(\mathbf o) \]

    • 对于不同的出射方向 \(\mathrm o\) ，得到一个Transport matrix。

    PRT2

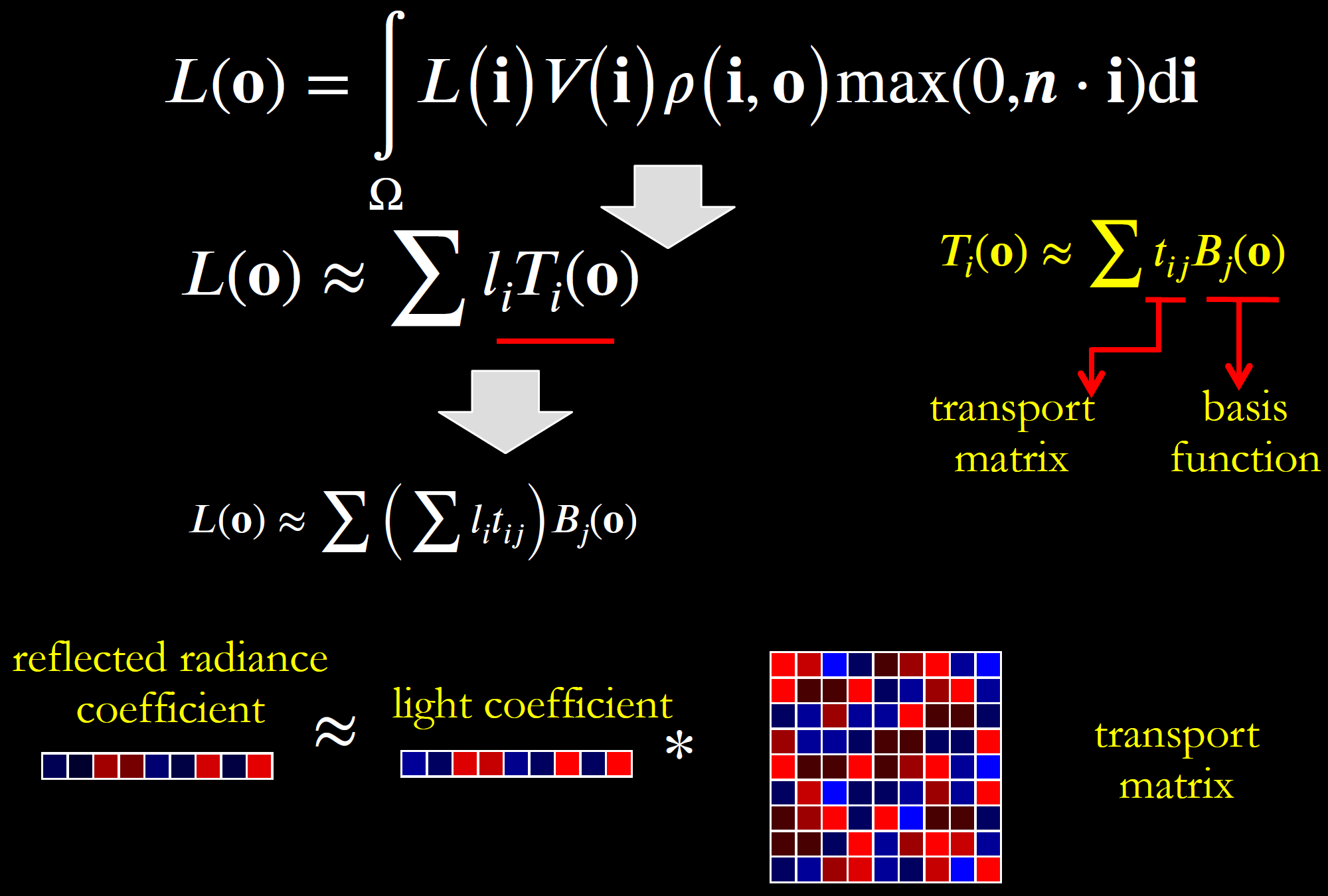
    • 代价：存储的Transport matrix，且一般用五阶SH，因此存储量大；且渲染需要计算向量与矩阵乘，相对复杂。

  • Transport Paths

    • \(LE\) : Light -> Eye
    • \(LGE\) : Light -> Glossy -> Eye
    • \(L(D|G)^*E\)
    • \(LS^*(D|G)^*E\) \(LSDE\) Caustics “焦散”（翻译不好）
    • 可以预计算任意复杂的Light Transport

  • 另一种理解 \(T_i\approx\int_{\Omega}B_i(\mathbf i)V(\mathbf i)\max(0,\mathbf n\cdot\mathbf i)\,\mathrm d\mathbf i\) 中，将 \(B_i(\mathbf i)\) 视作入射光，预计算过程就相当于用这些“奇怪”的光照渲染场景。

    PRT3

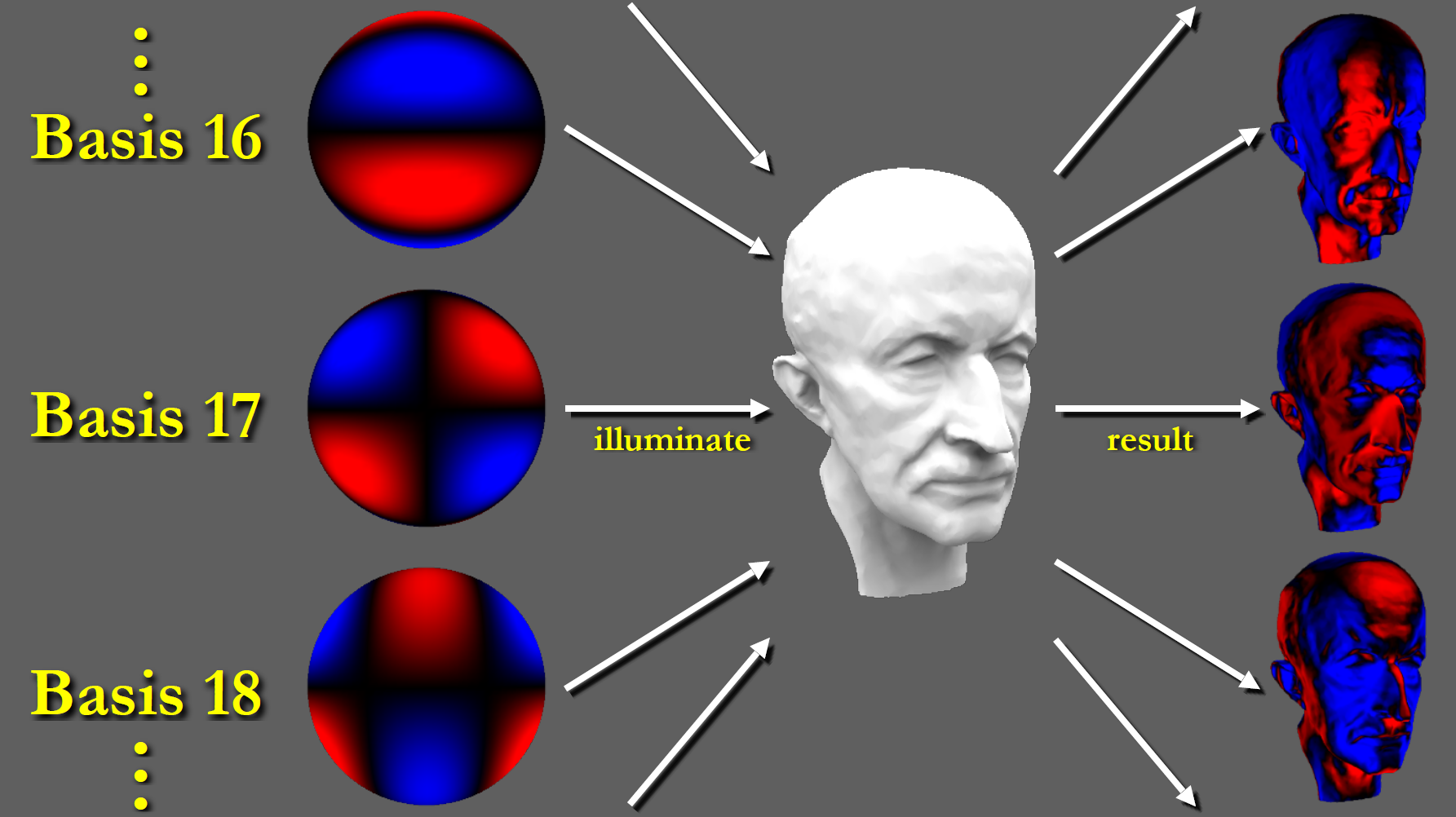
  • 限制

    • SH只适合描述低频信息（镜面反射）
    • 固定场景
    • 大量的预计算和存储

  • 进一步的工作

    • 新型基函数
    • 两项点乘 -> 三项相乘
    • 动态场景
    • 动态材质
    • 透明材质、头发、…
    • 预计算 -> 不做预计算的解析解
    • …

  • 其他基函数

    • 小波 Wavelet
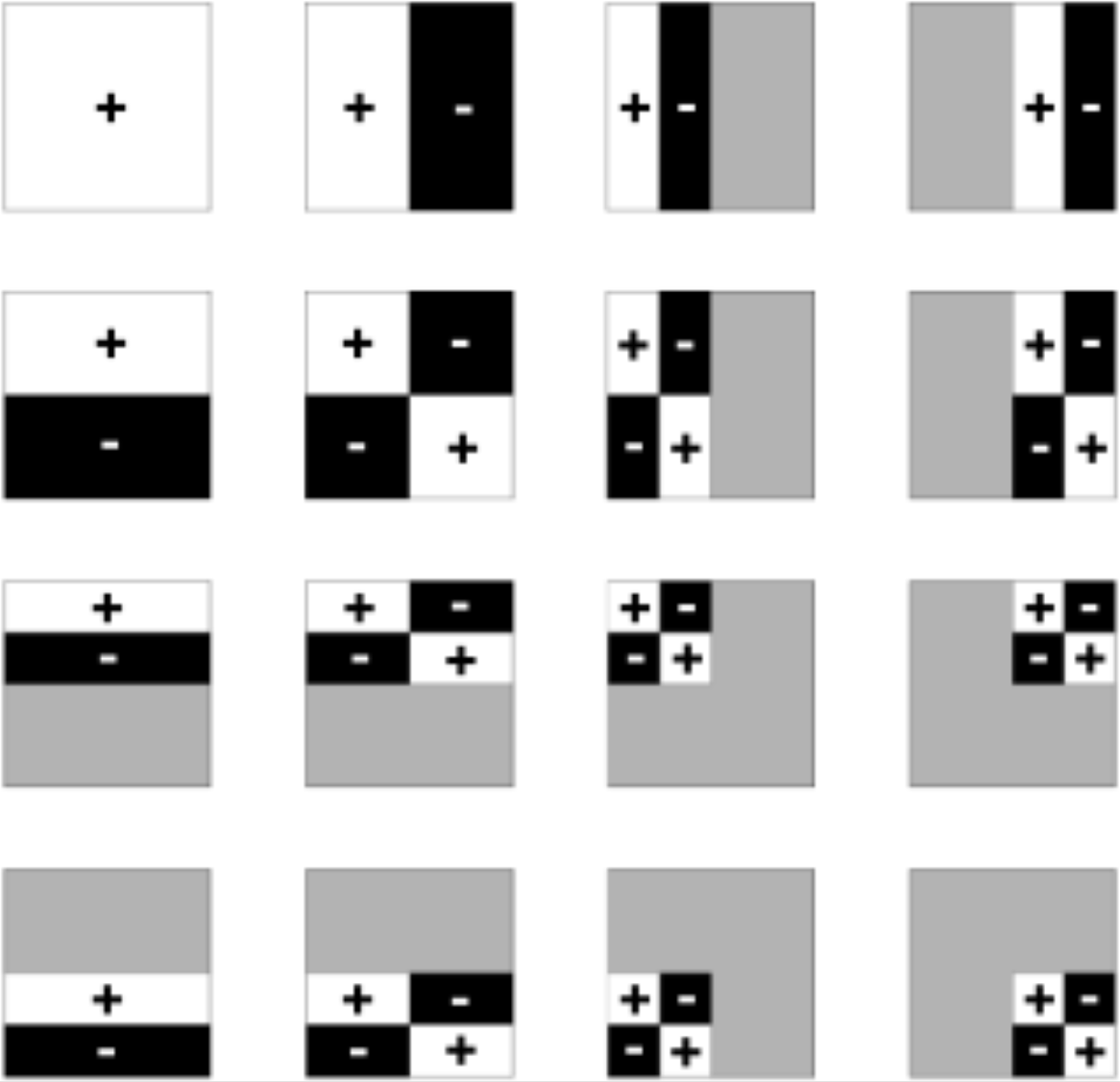
      • 二维小波 Wavelet1
      • 投影
        • 小波变换
        • 大量系数为零 -> 用于压缩
      • 全频率的表示
      • 用Cubemap存储光照，6张图每张做小波变换
      • 把低频存在图左上1/4，剩下3/4存高频，对低频的1/4图递归地做这样的操作 -> 发现高频信息很少，非常适合压缩 Wavelet2
      • 问题：不支持快速旋转
    • Zonal Harmonics
    • Spherical Gaussian
    • Piecewise Constant