Lecture08 Animation System - Basics

挑战：

  • 不能预设玩家的行为，考虑动画与Gameplay的互动，与环境的交互
  • 实时，计算和存储开销
  • 真实感（表情、Ragdoll、Motion Matching …）

2D Animation

Sprite Animation
  • 逐帧绘制，循环播放
  • Sprite-like animation technique in pseudo-3D game
    • 《Doom》 绘制各个视角的sprite，做伪3D
  • Sprite Animation in Modern Game
Live2D
  • 把角色/主体的每个元素作为独立图元 eg.眼睛、鼻子、嘴巴 L08_Live2D1
  • 仿射变换 L08_Live2D2
  • 图元的前后遮挡由深度决定
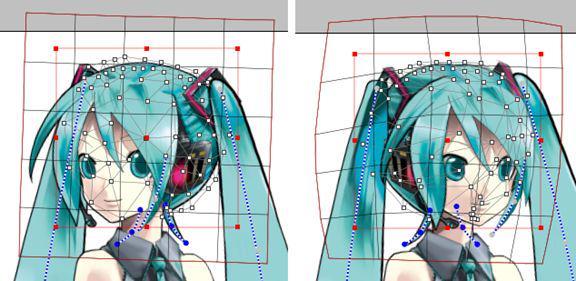
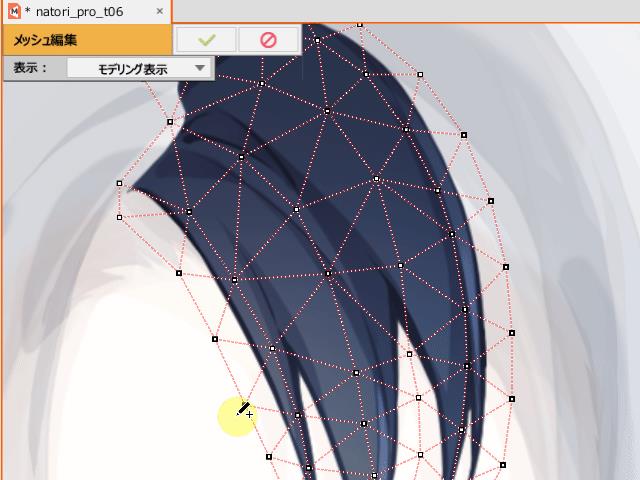
  • 每一个图元有控制网格 L08_Live2D3
  • Key frame
2D Skinned Animation 2D蒙皮动画

3D Animation

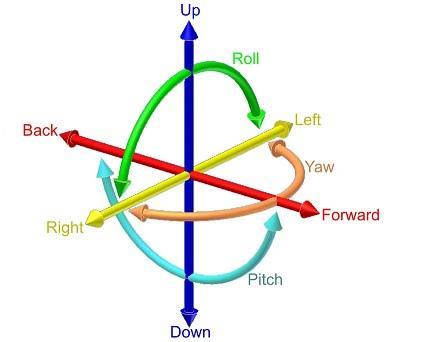
DoF, Degrees of Freedom 自由度 6DoF + Translation X Y Z + Rotation Pan/Yaw Tilt/Pitch Roll L08_DoF

Rigid Hierarchical Animation 基于刚体的层次结构动画
  • “皮影戏”
  • 直接连接Mesh，会导致Mesh互相产生穿插
Per-vertex Animation
  • 旗帜、布料、流体等（从物理烘焙而来的顶点动画实现）
  • VAT, Virtual Animation Texture：用贴图存储顶点
Morph Target Animation
  • 顶点动画的变种
  • 顶点带有权重，邻近顶点相互影响
3D Skinned Animation 2D蒙皮动画 （见下章）
Physics-based Animation
  • Ragdoll
  • 布料和流体
  • IK, Inverse kinematics 反向动力学
Animation 创作方式
  • Key frame
  • 动作捕捉

Skinned Animation Implementation

怎样将Mesh运动起来
  • 创建一个绑定姿态的Mesh
  • 创建绑定骨骼Skeleton
  • 刷定点权重（蒙皮）
  • 骨骼动画
  • 顶点按骨骼动画和蒙皮权重运动

Different Spaces

  • Local Space 每一个骨骼节点
  • Model Space
  • World Space
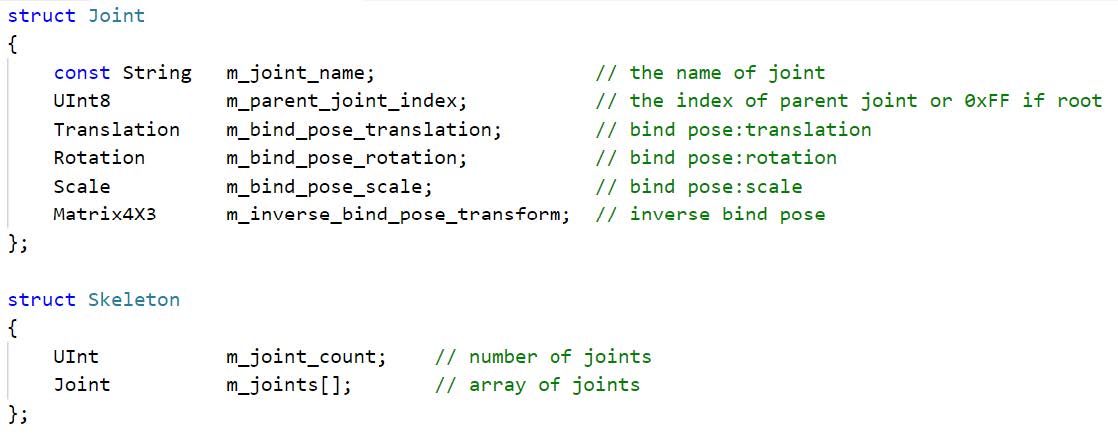
骨骼

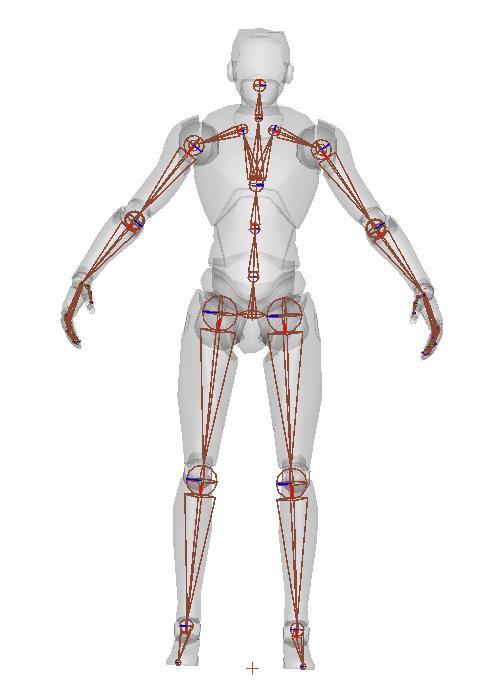
  • Humanoid 两足动物 L08_HumanoidSkeleton

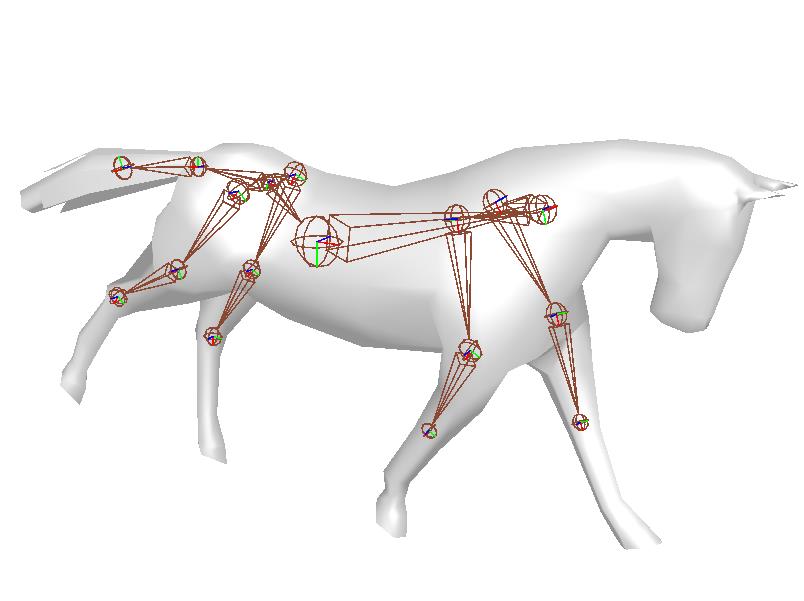
  • Non-humanoid 四足动物 L08_Non-humanoidSkeleton

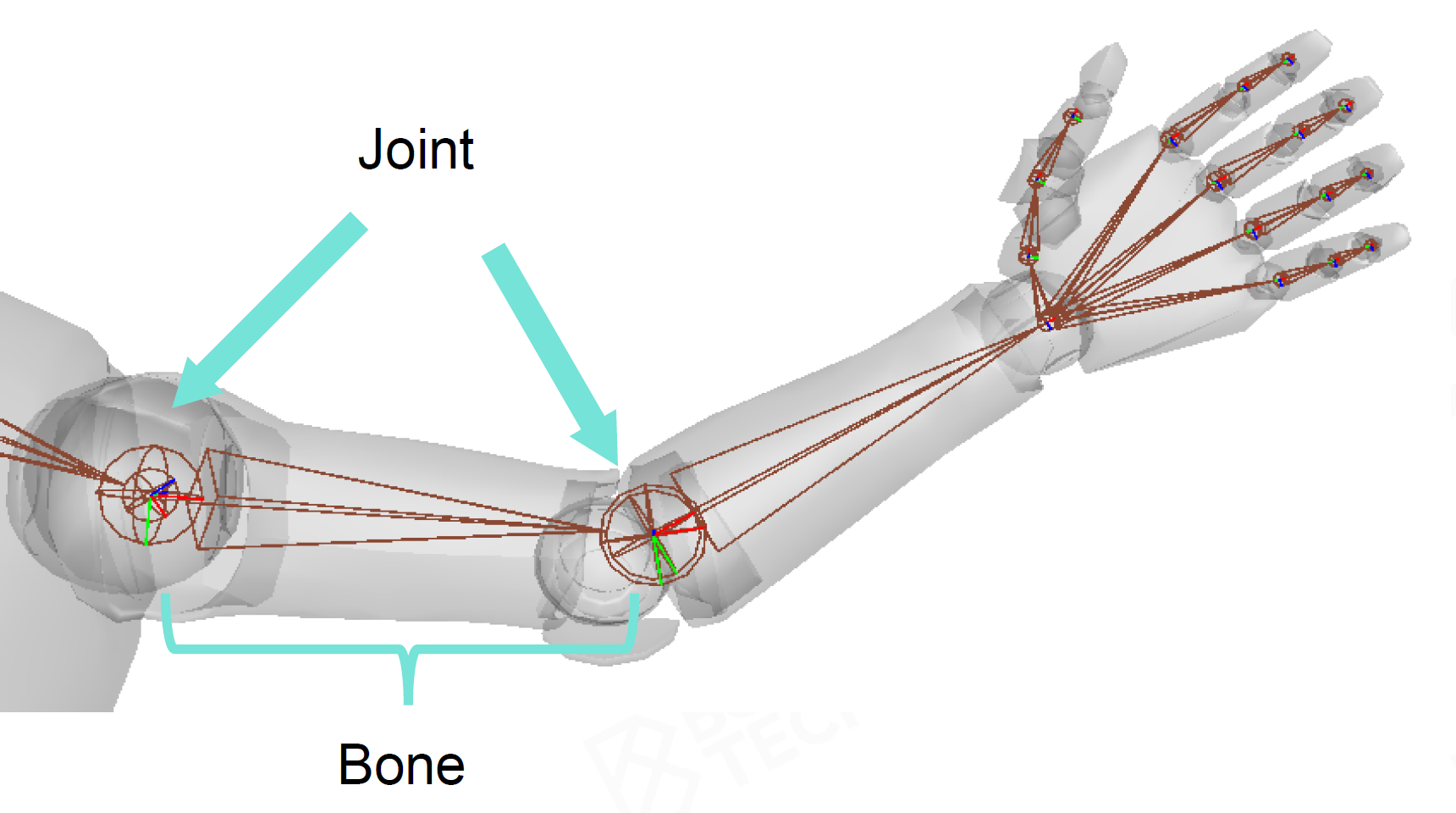
  • Joint 和 Bone 关节和骨段，存储/处理的是Joint L08_JointVsBone

  • 真实情况中的附加骨骼

    • 复杂的表情
    • 披风、翅膀、武器等外饰
    • eg. 武器可能是单个Joint绑定在手上

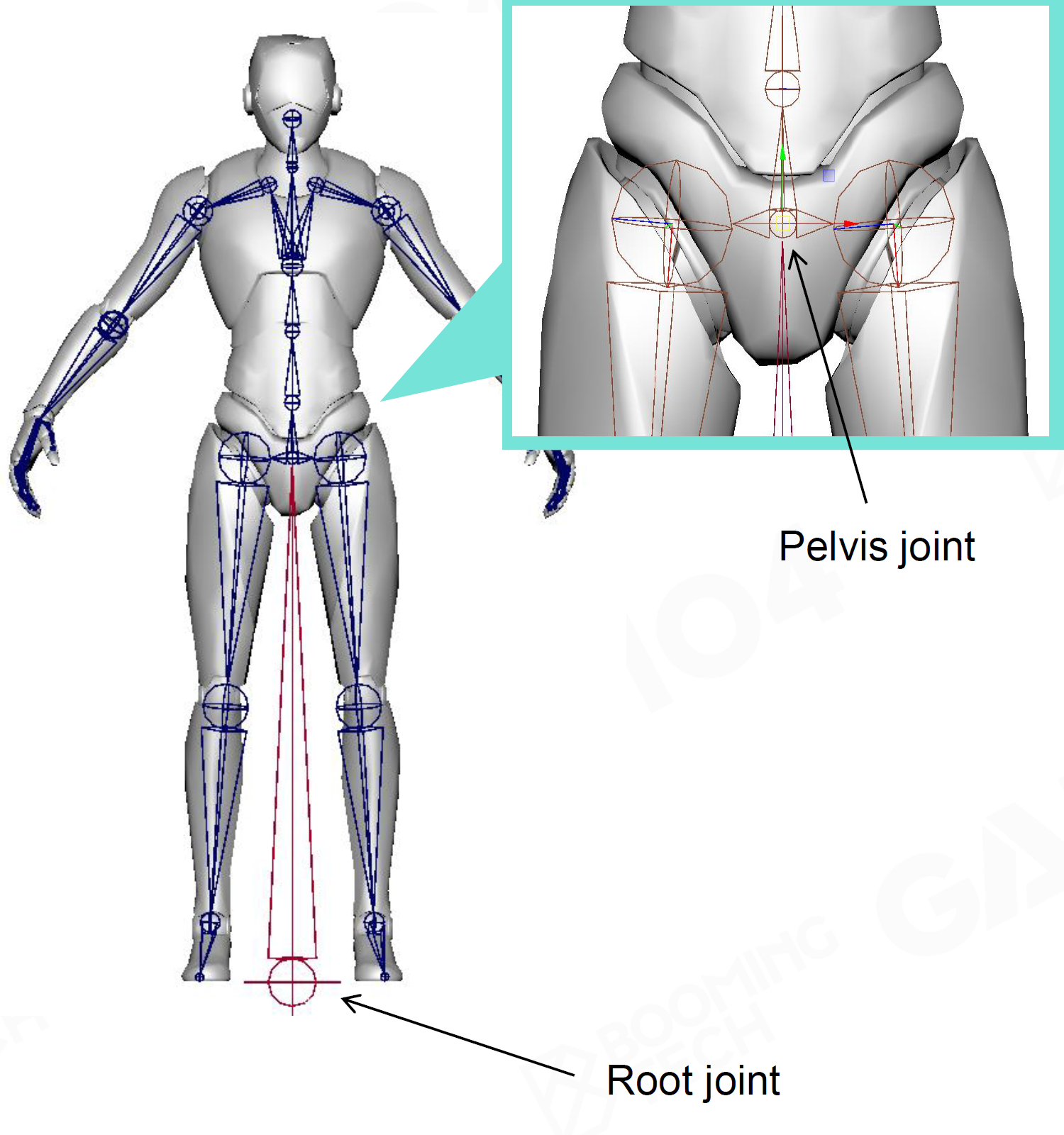
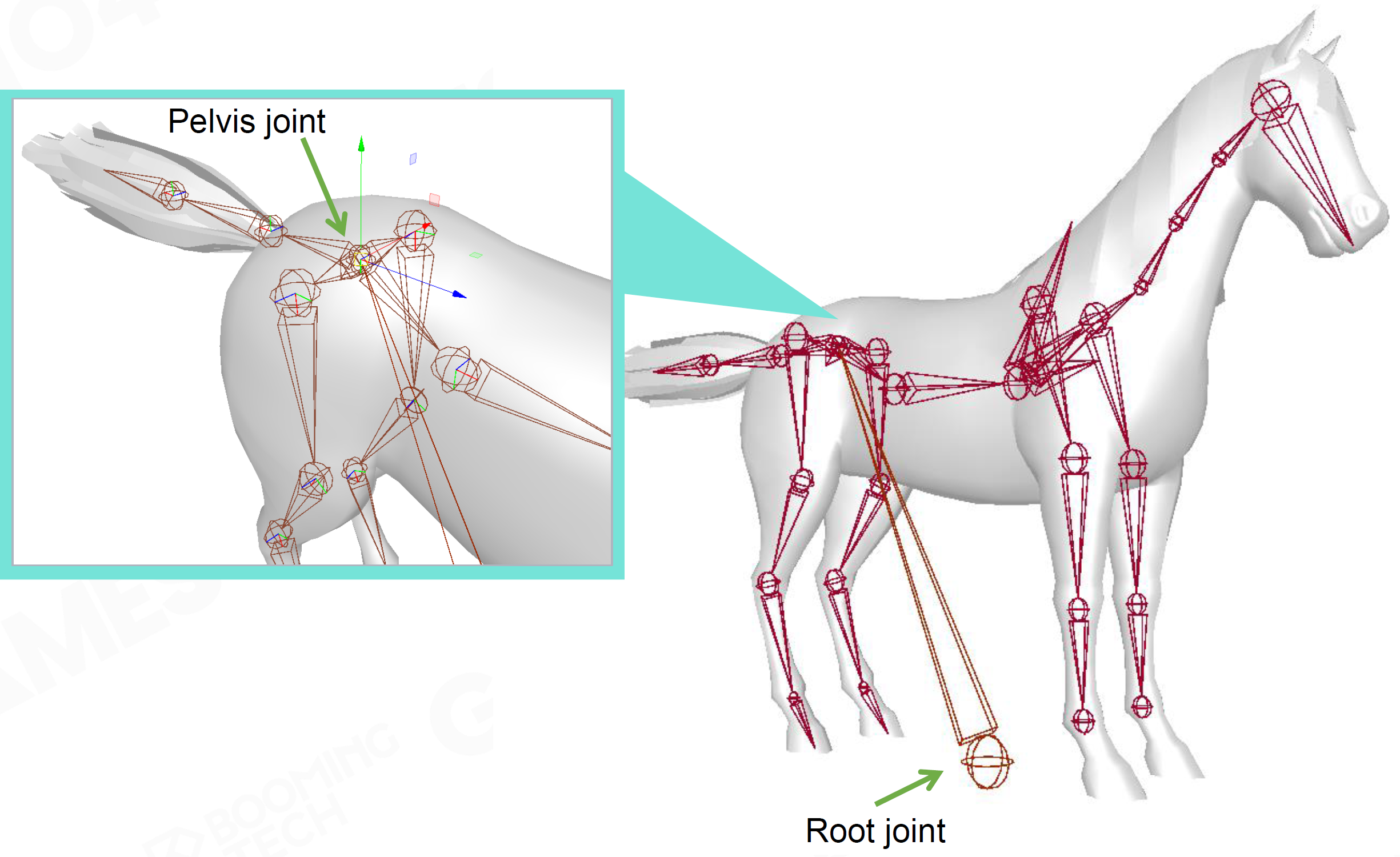
  • Root节点 一般在地面 L08_RootJoint1L08_RootJoint2

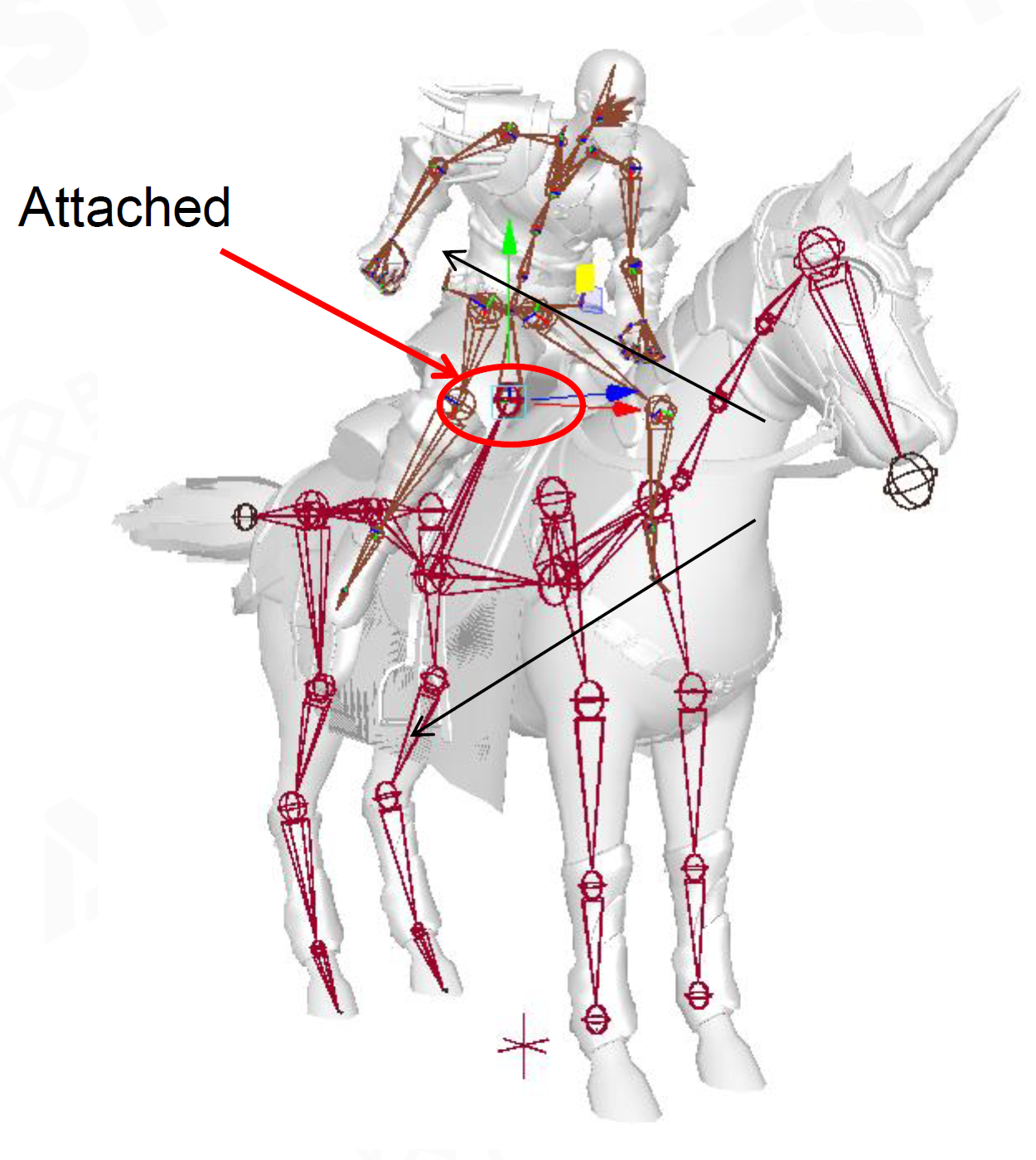
  • 物体之间的骨骼Attach，骑马/开车等情况 L08_AttachJoint

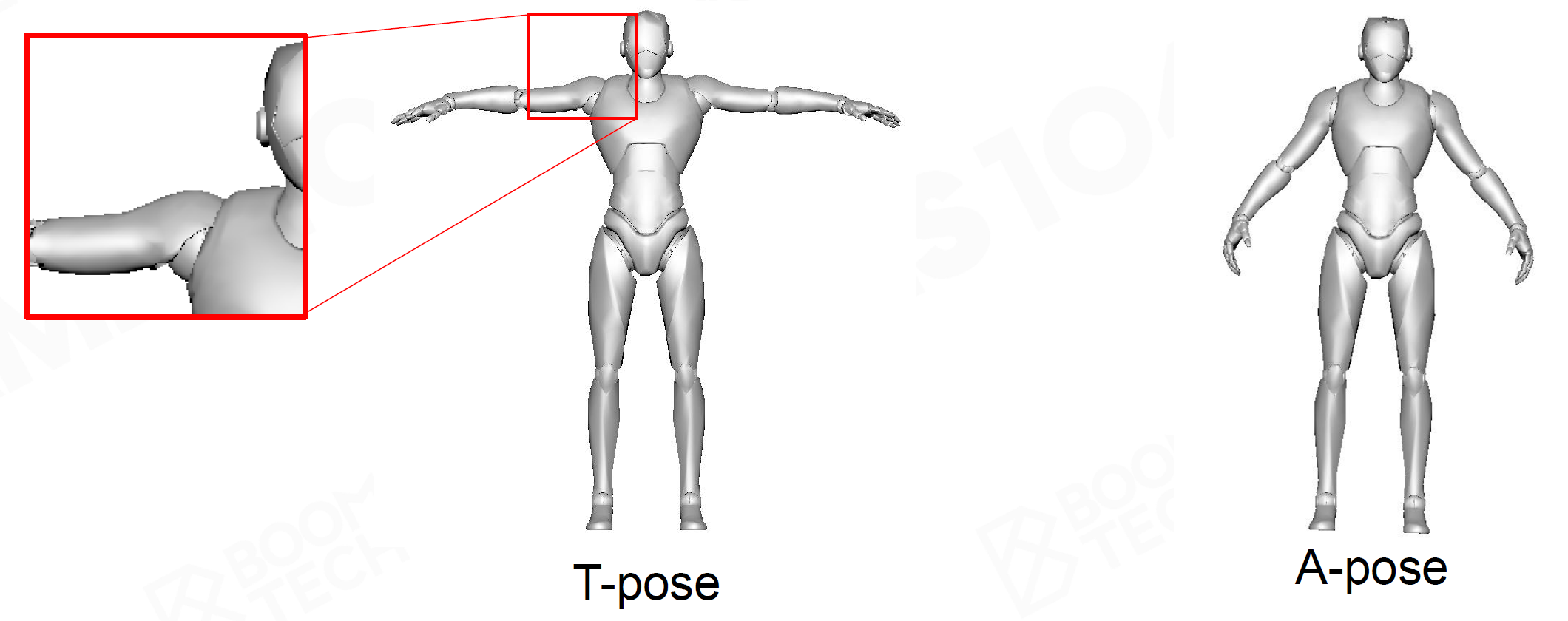
  • 绑定初始状态 T-Pose和A-Pose

    • T-Pose肩部受到挤压，精度不够
    • 目前大多采用A-Pose L08_TA-Pose

  • Pose：一个骨骼的状态

    • Joint Pose (9DoF)

      • Position
      • Orientation
      • Scale > Math of 3D Rotation （略）

    • Affine Matrix 仿射矩阵 \[ M=R_{HM}T_{HM}S_{HM}=\begin{bmatrix}SR & T\\0&1\end{bmatrix} \]

    • 从Local Space到Model Space \[ M_J^{\rm Model}=\prod_{j=J}^0 M_{p(J)}^{\rm Local} \]

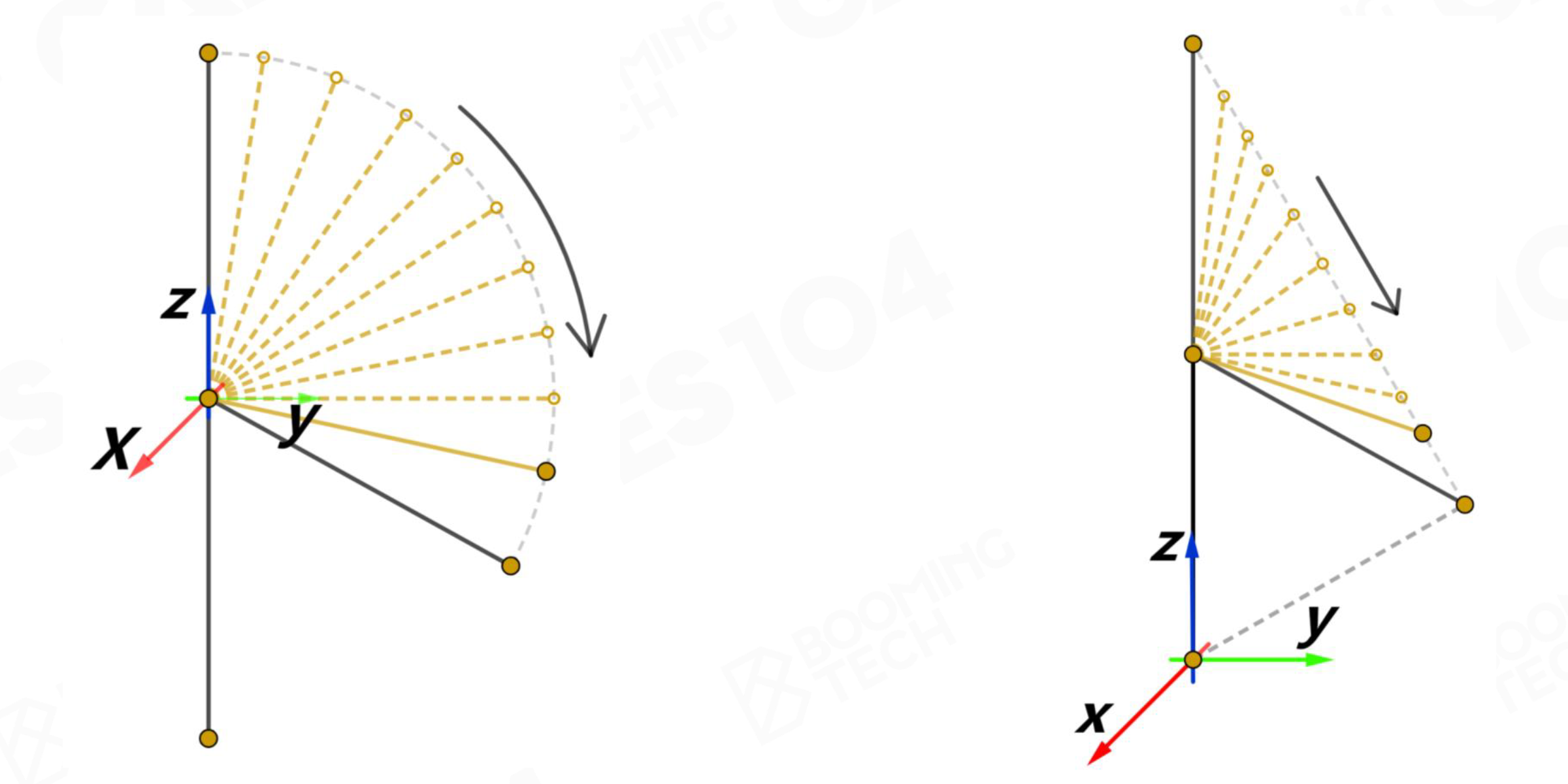    • Interpolation L08_JointInterpolation 左：Local Space 右：Model Space 故在Local Space进行插值，再转换至Model Space

Skin - 蒙皮怎样运动

  • Skinning Matrix

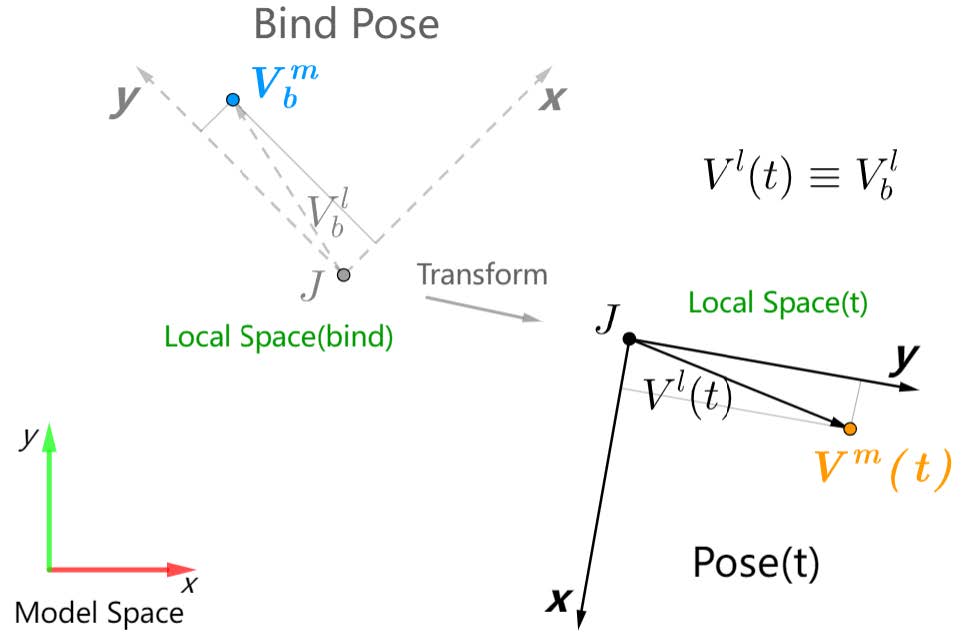
    • \(V^{\rm Local}(t)\)：顶点 \(V\) 在Local Space，\(t\) 时间的位置： \[ V^{\rm Local}(t)\equiv V_b^{\rm Local}=(M_{b(j)}^{\rm Model})^{-1}\cdot V_b^{\rm Model} \] L08_SkinningMatrix

    • \(M_J^{\rm Model}(t)\)：Joint \(J\) 在Model Space，\(t\) 时间的pose： \[ M_J^{\rm Model}(t)=\prod_{j=J}^0 M_{p(j)}^{\rm Local}(t) \]

    • \(V^{\rm Model}(t)\)：顶点 \(V\) 在Model Space，\(t\) 时间的位置： \[ V^{\rm Model}(t)=M_J^{\rm Model}(t)\cdot V_J^{\rm Local}=M_J^{\rm Model}(t)\cdot(M_{b(j)}^{\rm Model})^{-1}\cdot V_b^{\rm Model} \]

    • Skinning Matrix \[ K_J=M_J^{\rm Model}(t)\cdot(M_{b(j)}^{\rm Model})^{-1} \]

  • Skinning Matrix Palette

    • 存储每个Joint的Skinning Matrix

    • Model Space to World Space \[ K_J'=M^{\rm World}\cdot M_J^{\rm Model}(t)\cdot(M_{b(j)}^{\rm Model})^{-1} \] 存储该Skinning Matrix’

    • Bind Pose Matrix的逆需提前计算存储，以提高效率 L08_InverseBindPoseMatrix

  • Weighted Skinning with Multi-joints

    • 加权平均（一般不超过4个），加权总和为1

    • Weighted Skinned Blend

      • 顶点 \(V\) 关于Joint \(J_i\) 的Local Space to Model Space： \[ V_{J_i}^M(t)=K_{J_i}(t)\cdot V_{b_{J_i}}^M \]

      • 顶点 \(V\) 在Model Space： \[ V^M(t)=\sum_{i=0}^{N-1}W_i\cdot V_{J_i}^M(t) \]

Clips 动画片段

  • Interpolation

    • LERP - Translation / Scale \[ f(x)=(1-\alpha)f(x_1)+\alpha f(x_2)\\ \alpha=\dfrac{x-x_1}{x_2-x_1},\,x_1<x_2,\,x\in[x_1,x_2];\quad f(x):T(t),S(t) \]

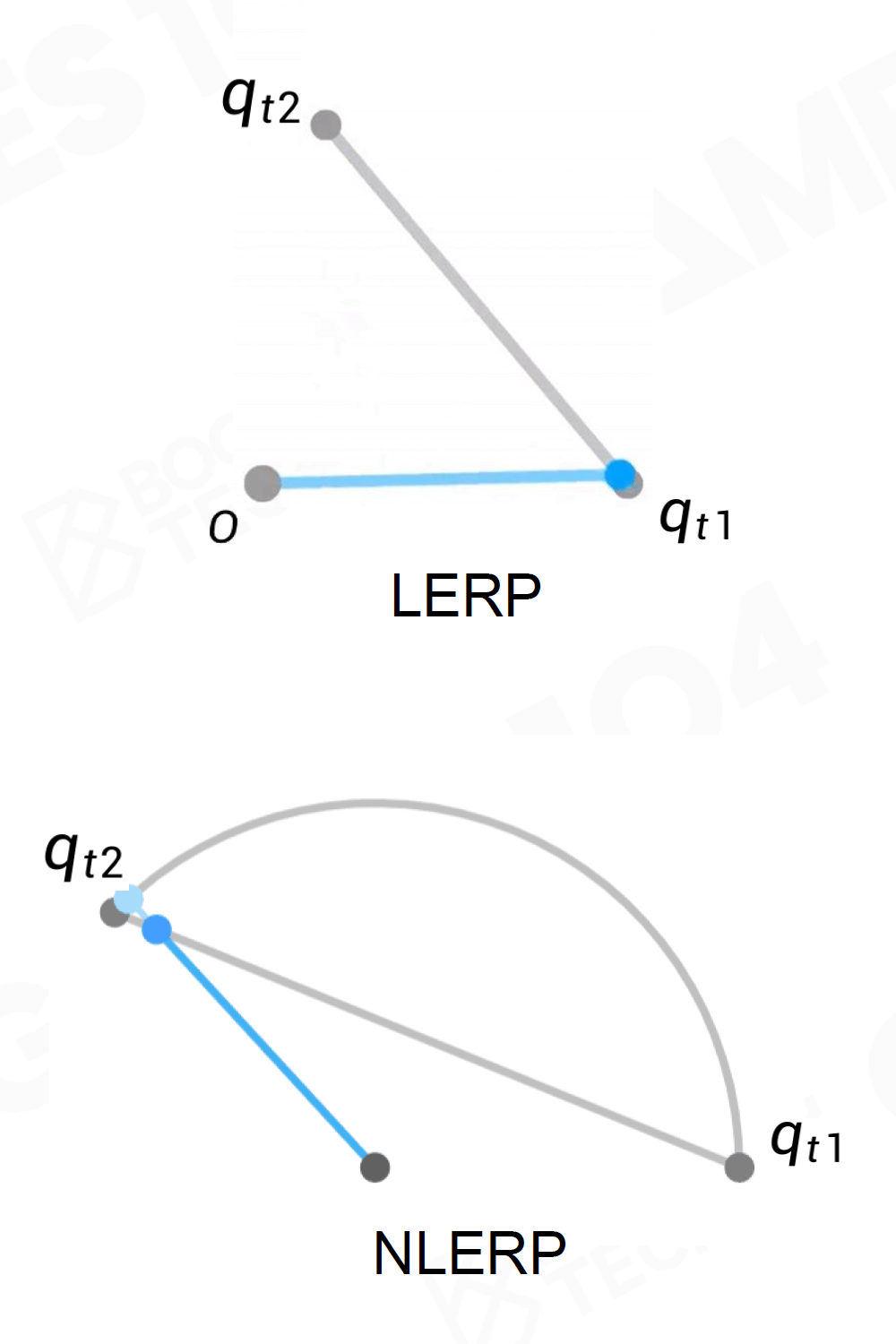
    • NLERP for Quaternion - Rotation L08_LerpVsNLerp

      • Linear Interpolation \[ q_t={\rm Lerp}(q_{t_1},q_{t_2},t)=(1-\alpha)q_{t_1}+\alpha q_{t_2}\\ \]

      • Normalization \[ q_t'={\rm NLerp}(q_{t_1},q_{t_2},t)=\dfrac{(1-\alpha)q_{t_1}+\alpha q_{t_2}}{\|(1-\alpha)q_{t_1}+\alpha q_{t_2}\|} \]

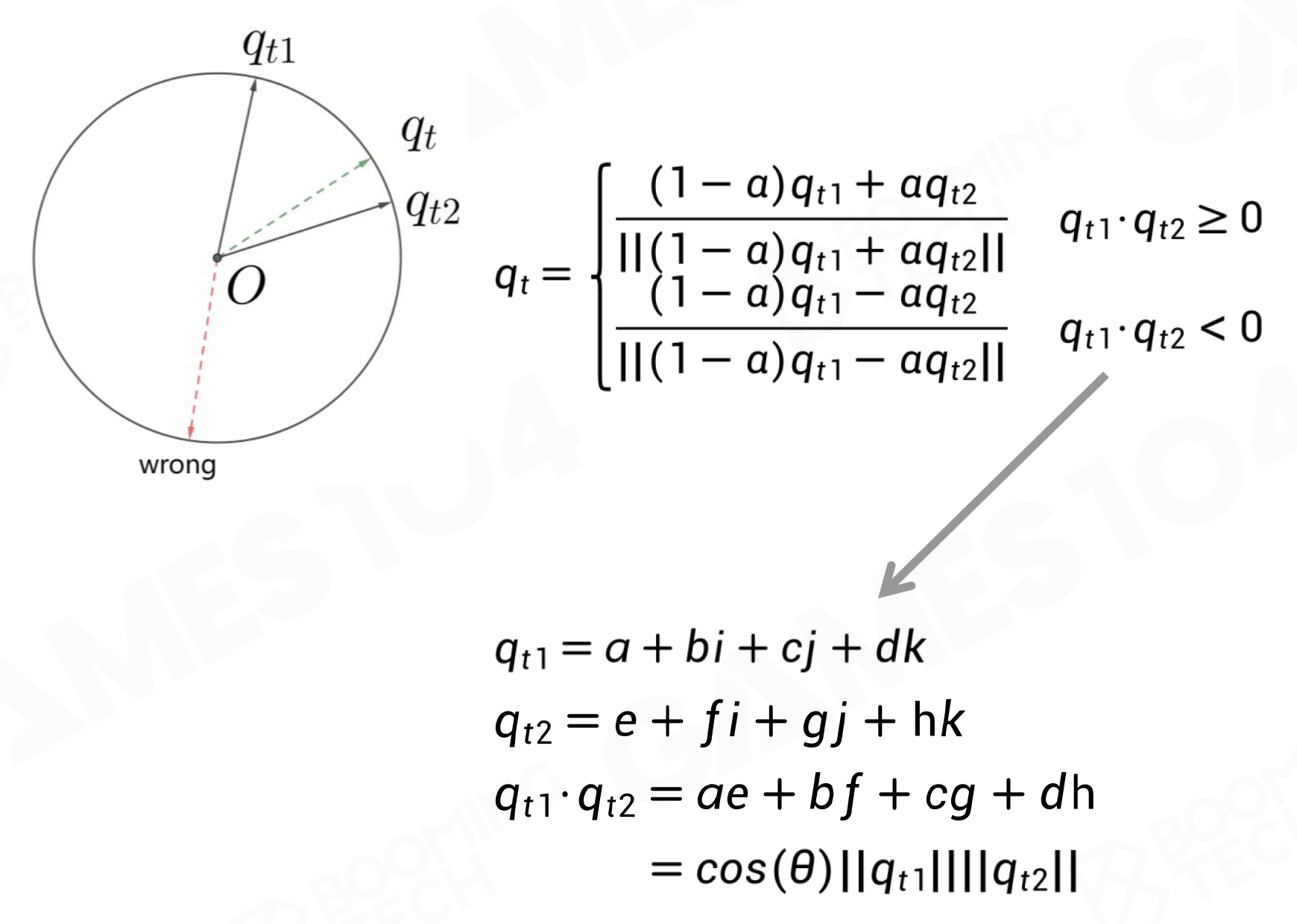
      • 最短路径 L08_ShortestPath

    • SLERP for Quaternion - Rotation

      • NLERP在弦上插值，故旋转不均匀；SLERP在球面上插值，但开销较大

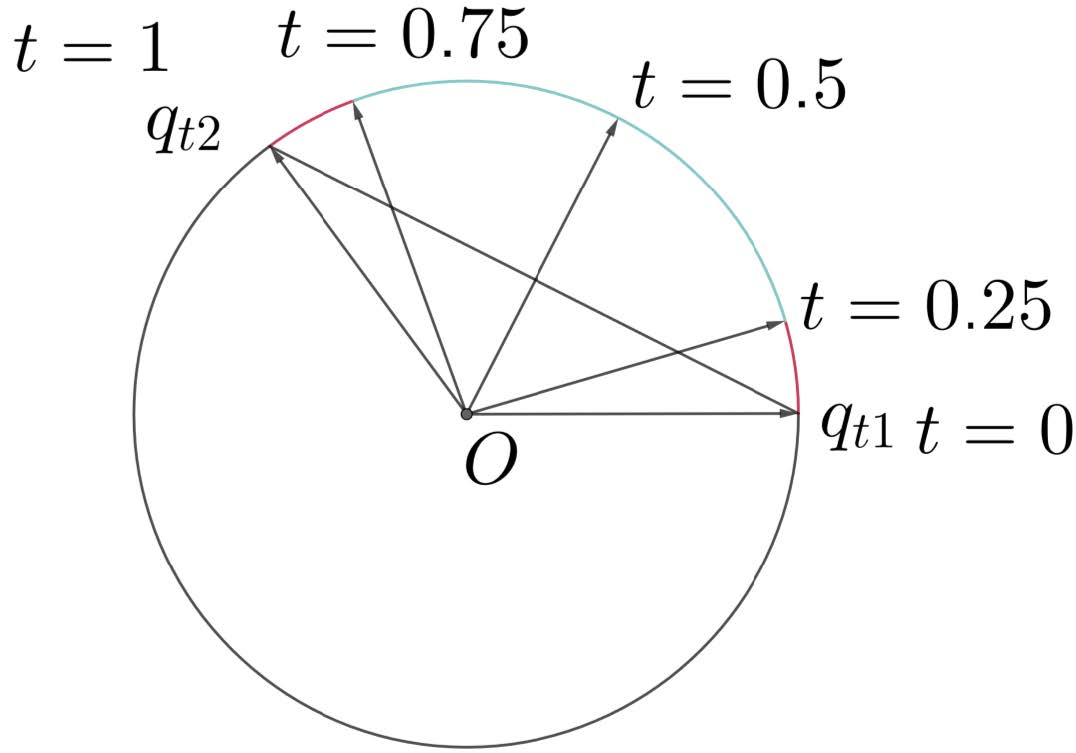
      • \[ q_t={\rm SLerp}(q_{t_1},q_{t_2},t)=\dfrac{\sin((1-t)\theta)}{\sin\theta}\cdot q_{t_1}+\dfrac{\sin(t\theta)}{\sin\theta}\cdot q_{t_2}\\ \theta=\arccos(q_{t_1}\cdot q_{t_2}) \] L08_SLERP

      • 一般设置阈值，插值角度小，则NLerp，插值角度非常大时使用SLerp

Simple Animation Runtime Pipeline

L08_SimpleAnimationRuntimePipeline

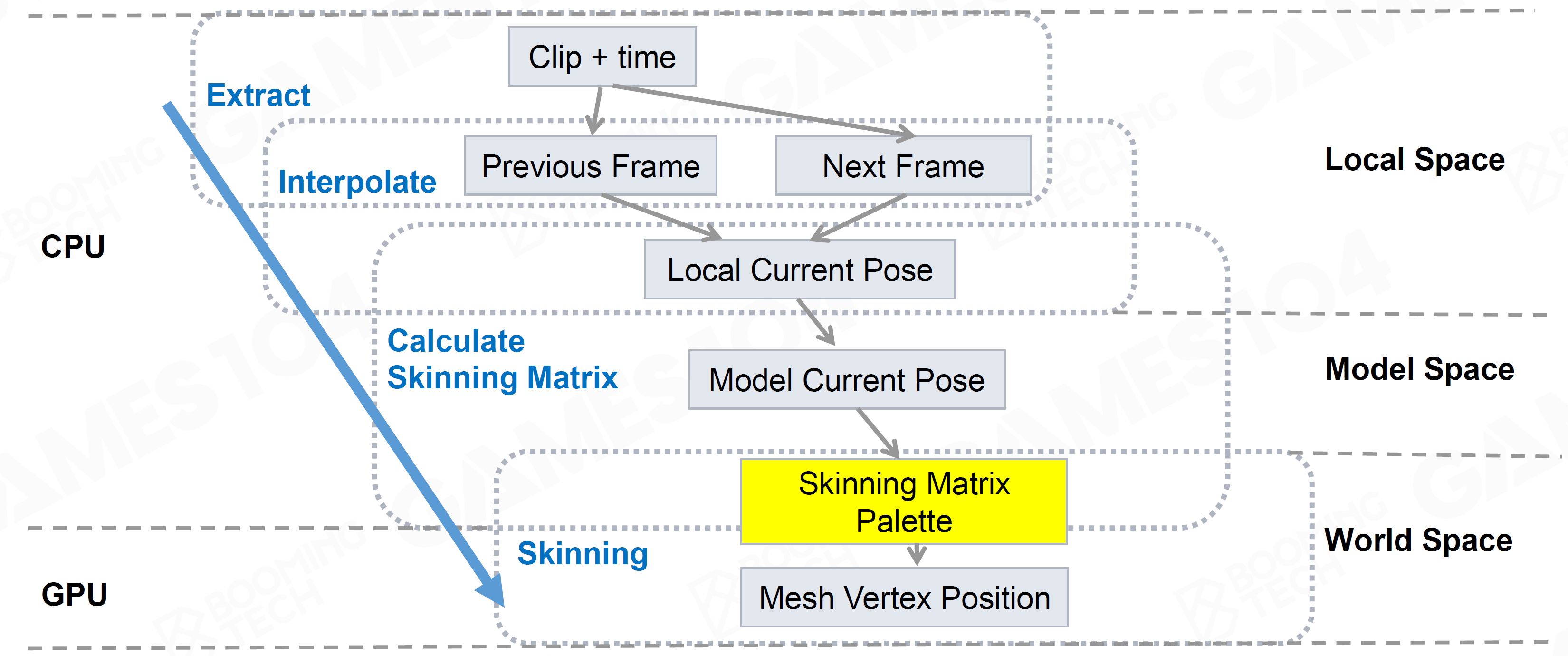
Animation Compression

  • 大部分数据不变

    • 部分Joint整个固定
    • 部分Joint的Translation/Rotation/Scale有部分保持不变（尤其是Translation和Scale）

  • DoF Reduction 减少不变的自由度

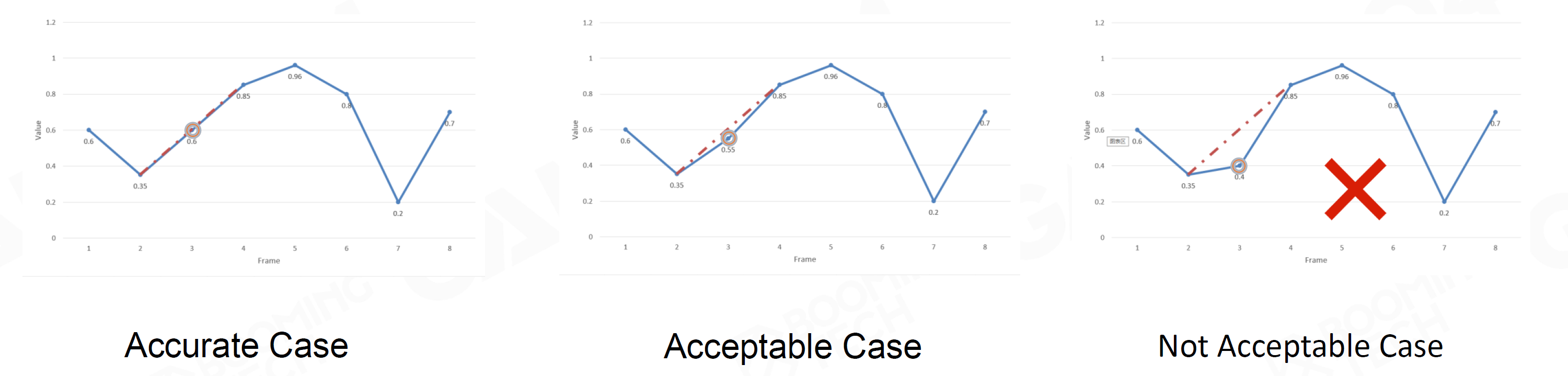
  • Keyframe 记录关键帧，其他帧插值

    • 使用插值方法测试

      • 若插值结果与真实结果差异小于阈值，则不记录为关键帧
      • 若插值结果与真实结果差异较大，则以真实结果为关键帧 L08_Keyframe1 L08_Keyframe2

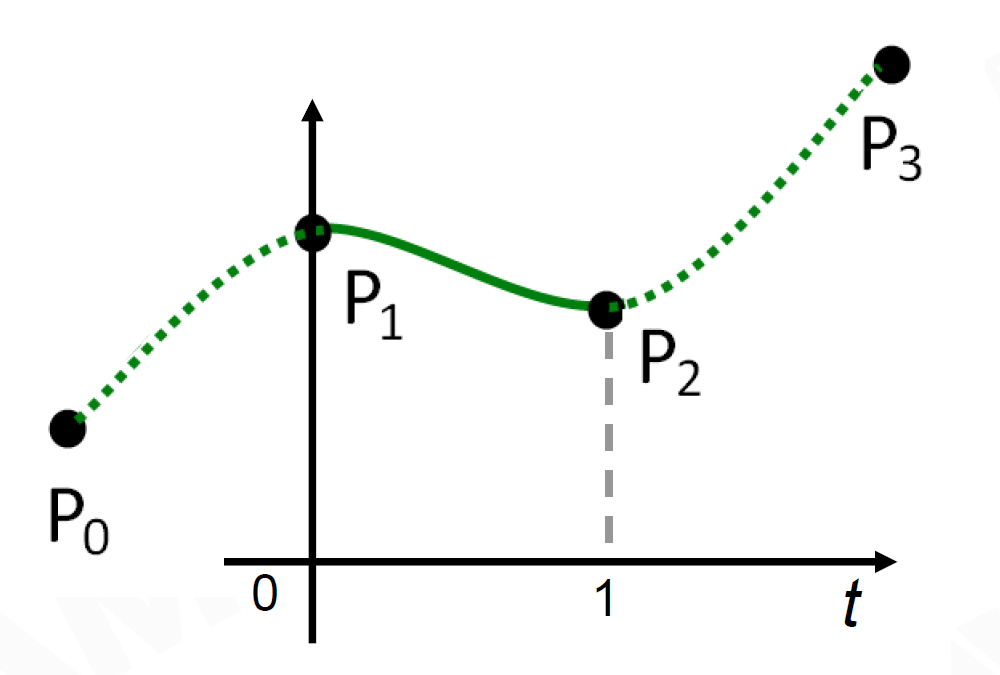
    • 采用Catmull-Rom Spline插值 —— 比线性插值更平滑（开销大但这里不是Runtime） \[ P(t)=\begin{bmatrix}1&t&t^2&t^3\end{bmatrix} \begin{bmatrix}0&1&0&0\\ -\alpha&0&\alpha&0\\ 2\alpha&\alpha-3&3-2\alpha&-\alpha\\ -\alpha&2-\alpha&\alpha-2&\alpha \end{bmatrix} \begin{bmatrix}P_0\\P_1\\P_2\\P_3\end{bmatrix} \] L08_Catmull-RomSpline

      • 减少了关键帧

  • Float Quantization

    • 32bit浮点存储量大
    • 将关键帧中数据的最小值、最大值mapping到 \([0, 1]\)
    • 所有数值mapping到16bit unsigned int来存储
    • 四元数的特性： \[ a^2+b^2+c^2+d^2=1,\,|a|\ge\max(|b|,|c|,|d|)\\ \Rightarrow b,c,d\in[-\frac{\sqrt 2}{2}, \frac{\sqrt 2}{2}] \] 因此，经验证四元数中除模最大的数 \(a\) 以外的三个数 \(b,c,d\) 可以用15bit精度表示，另有2bit表示哪个数最大；三个元共用48bit表示 L08_QuaternionQuantization
    • 经过压缩： L08_SizeReduction

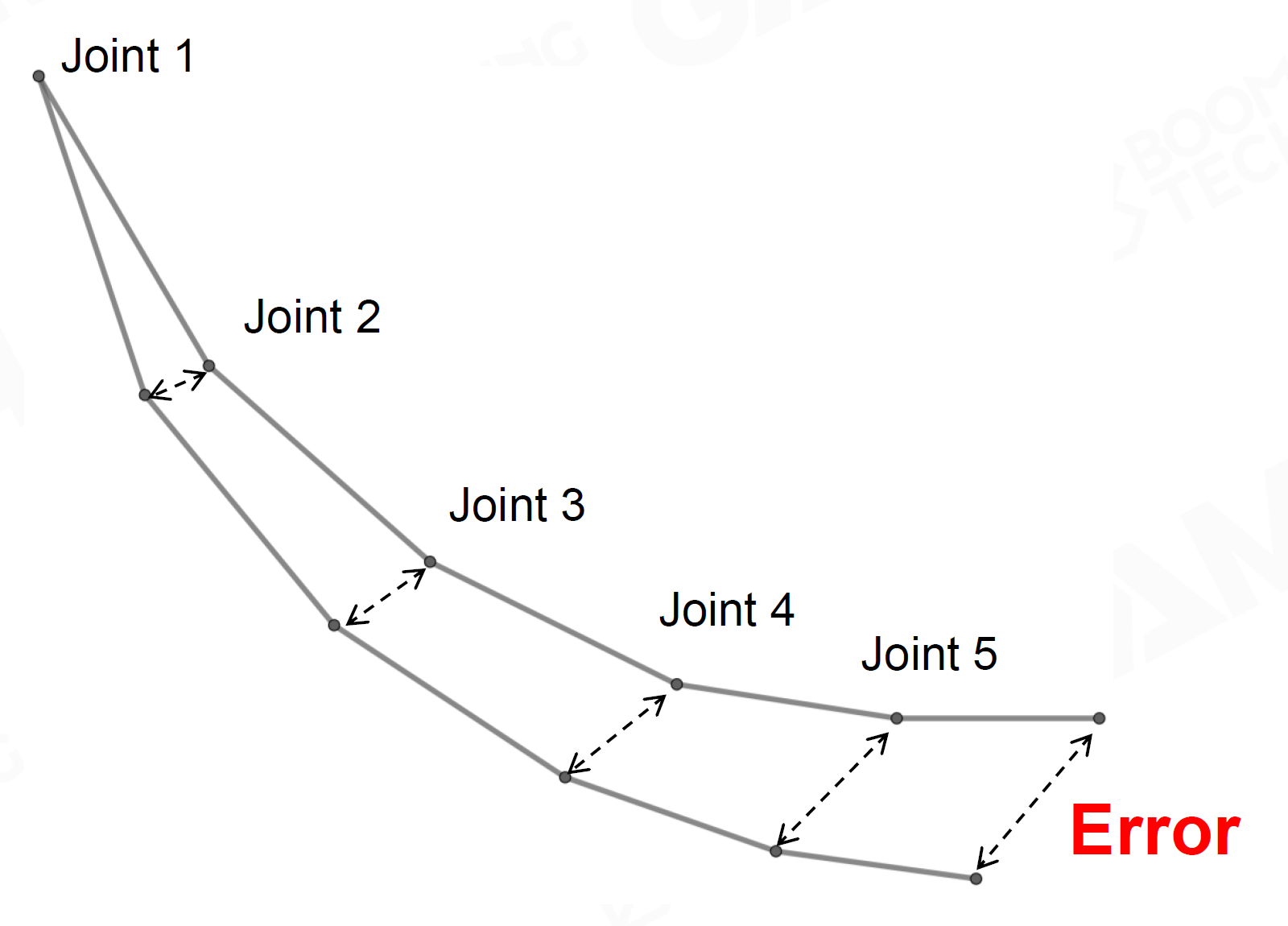
  • 误差传播 L08_ErrorPropagation

    • 结果会导致人物手部、手上武器等末端Joint发生抖动

    • 特殊情况需要高精度存储

      • 最简单的判定方法 —— 直接给误差设定阈值
      • Visual Error 视觉误差
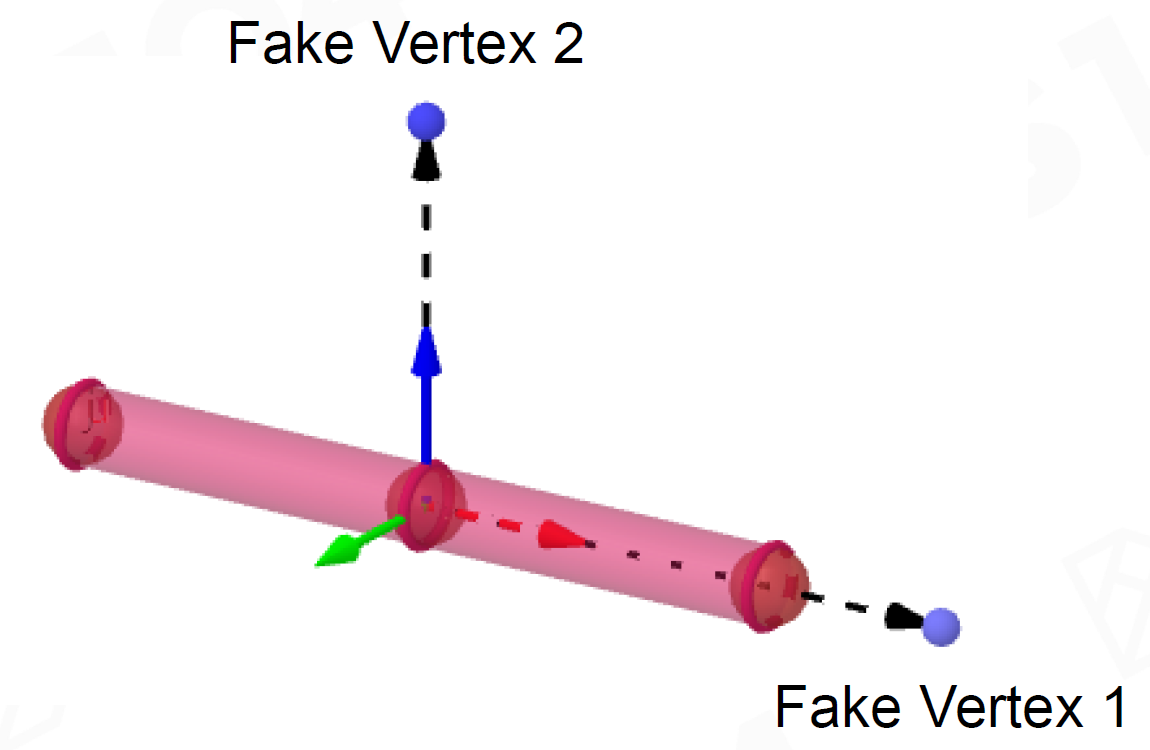
        • 为Joint在两个垂直方向设定两个Fake Vertex，计算运动后Fake Vertex的距离 L08_FakeVertex

  • 误差补偿

    • 处理方法：
      • 除Root外，每根bone上选一个点
      • 计算每根压缩后的bone的旋转，使标记点在Model Space中接近实际位置
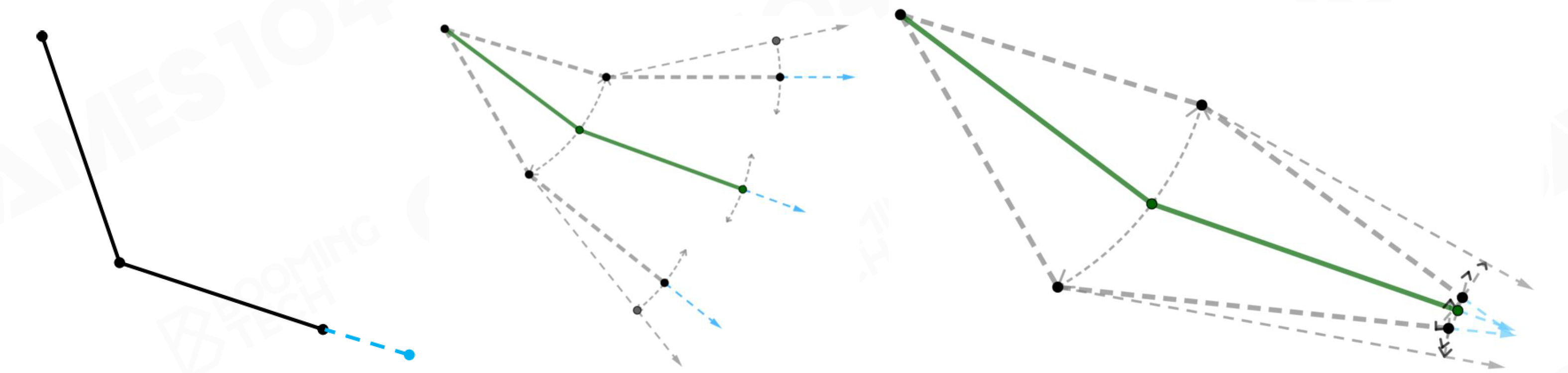
      • 增加一个旋转来补偿误差 L08_ErrorCompensation
    • 问题：末端骨骼的信息变成高频
    • 更新的方法：FIK, Forward Inverse Kinematics

Animation DCC

  • Mesh
    • 关节处Mesh更细分
  • Skeleton Binding 骨骼绑定
    • DCC的基础骨架
    • 增加武器等Gameplay中特殊的Joint
  • Skinning 蒙皮，刷权重
    • 自动计算 —— 结果会像橡皮
    • 手动部分校正权重
  • 设计关键帧动画
  • Root要保持在Model Space中不变
  • FBX File