这节课开始我们将花两节课的时间从粒子、刚体、流体三种系统,来简要介绍一些基于物理的动画的基本原理与实现,并给大家展示一些具体的制作方法和成果。
粒子系统
基于粒子的模型是基于物理的动画的一个基础模型,是拉格朗日方法中最典型的一种。这里的粒子系统个人认为广义地来说就是基于粒子的模型,是以粒子视点对物理现象做点采样的所有动画系统,但业界我们往往狭义地认为其典型就是特指由发射器发射大规模粒子、通过外力驱动运动、渲染成具体的无定形形象的系统。我们这一章的陈述主要还是以典型的粒子系统为主,会拓展些基于粒子的、但并不一定称为粒子系统的模型。
粒子系统一般用来表现雨、雪、火、烟、尘、沙尘暴、烟花、水花、喷雾等等“无定形现象(Amorphous Phenomena[1])”,当然也包括我们常见的一些“非物理现象”,诸如哥斯拉的吐息、猩红女巫的魔法光效等等,这些非物理现象同样要通过我们的物理系统去驱动粒子来产生这些效果。
一个粒子
在开始讲粒子系统之前,我们还是要讲一下一个粒子的运动:粒子的运动只有位移——就如我们中学物理中常做的质点模型一样,对一个粒子而言,所需要的动力学参数仅有、位置、速度、加速度、受力、质量等。在这之中,质量将受力与加速度联系为同一个概念,位置的变化(位移)是速度的积分、速度的变化又是加速度的积分。而且与中学物理不同的是,这里的每一个量都是三维空间中的向量了。
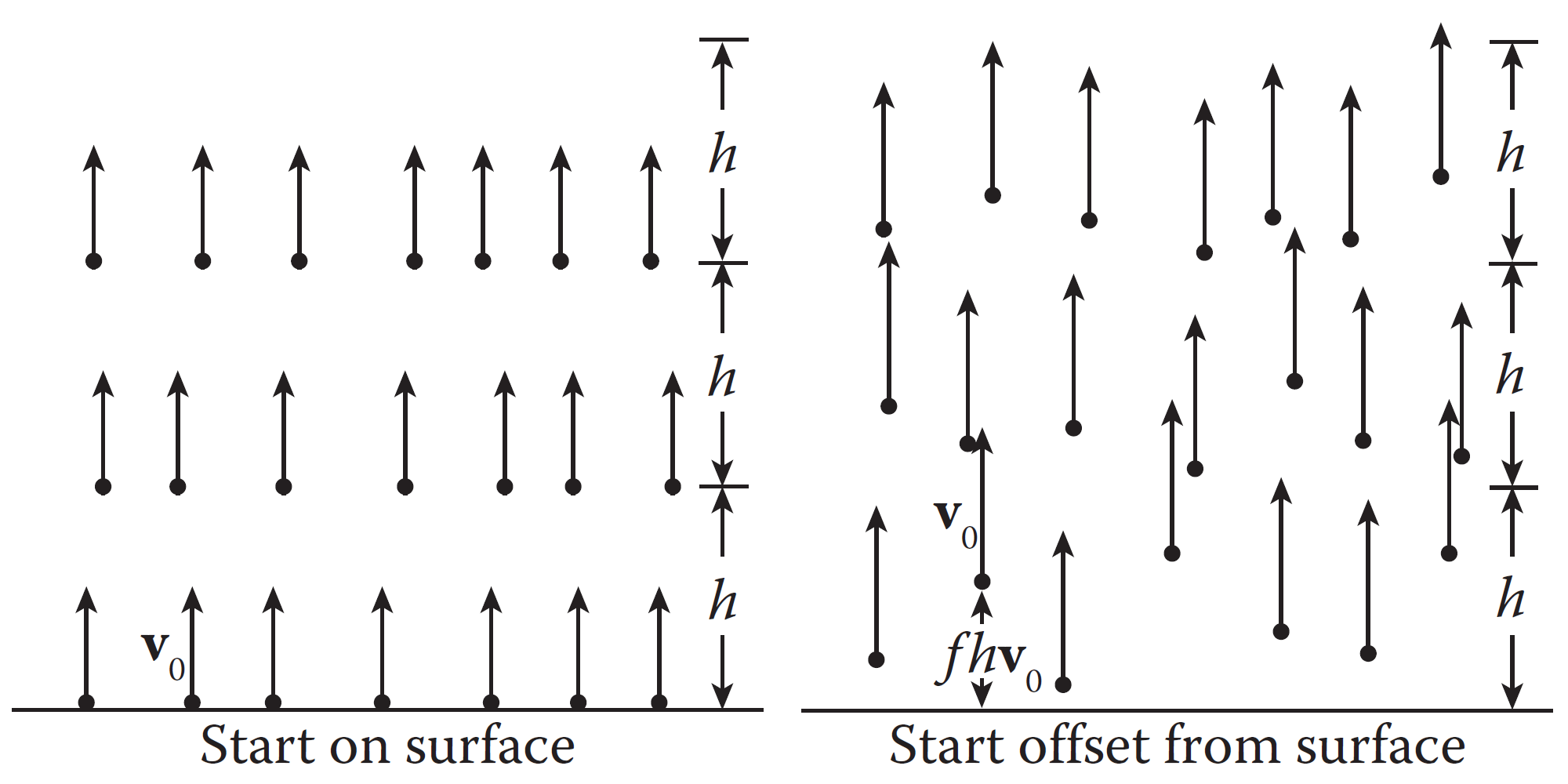
那么在这里,我们就第一次涉及到了时间积分概念的应用,也就是我们上节课刚刚讲过的如何在时间离散系统里做积分。
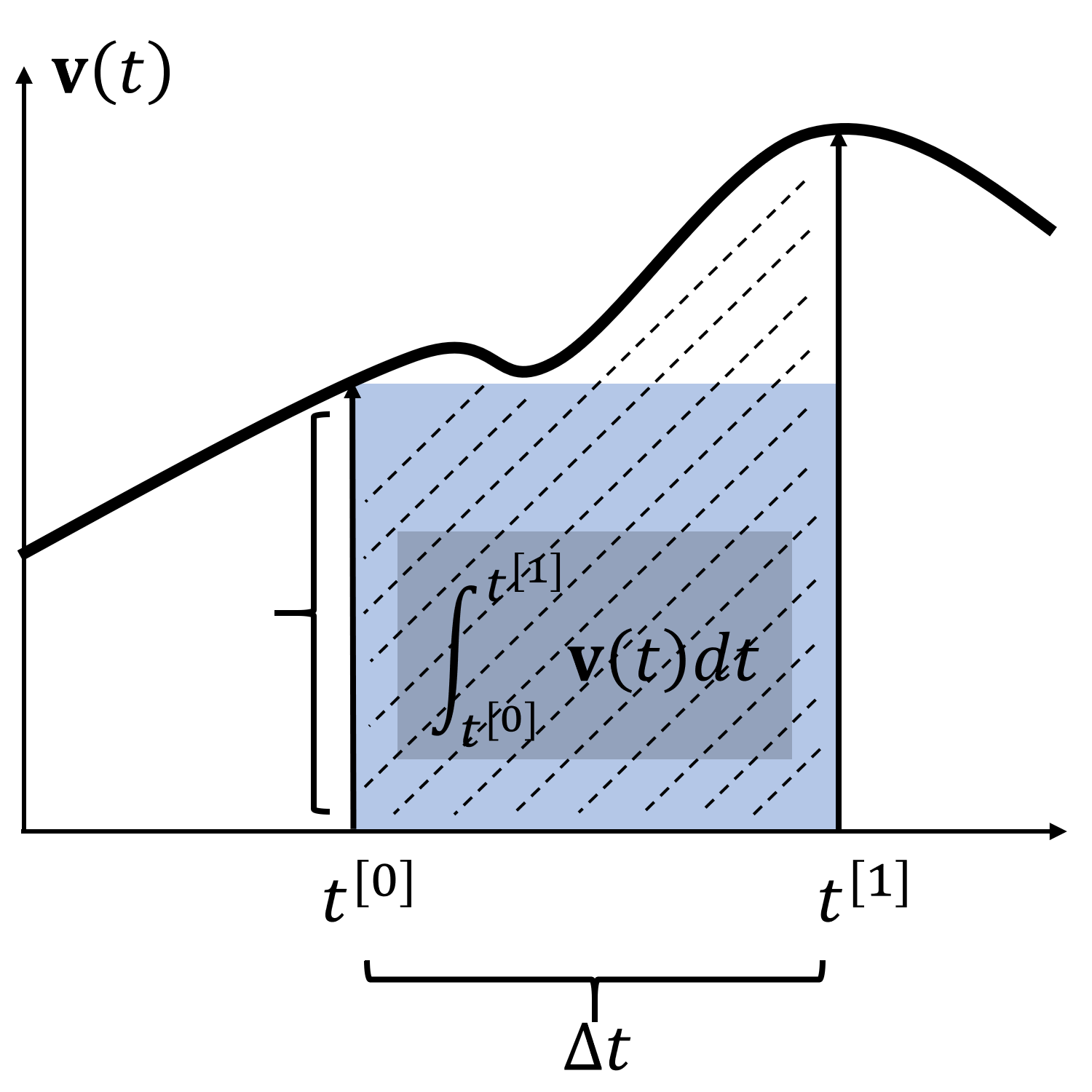
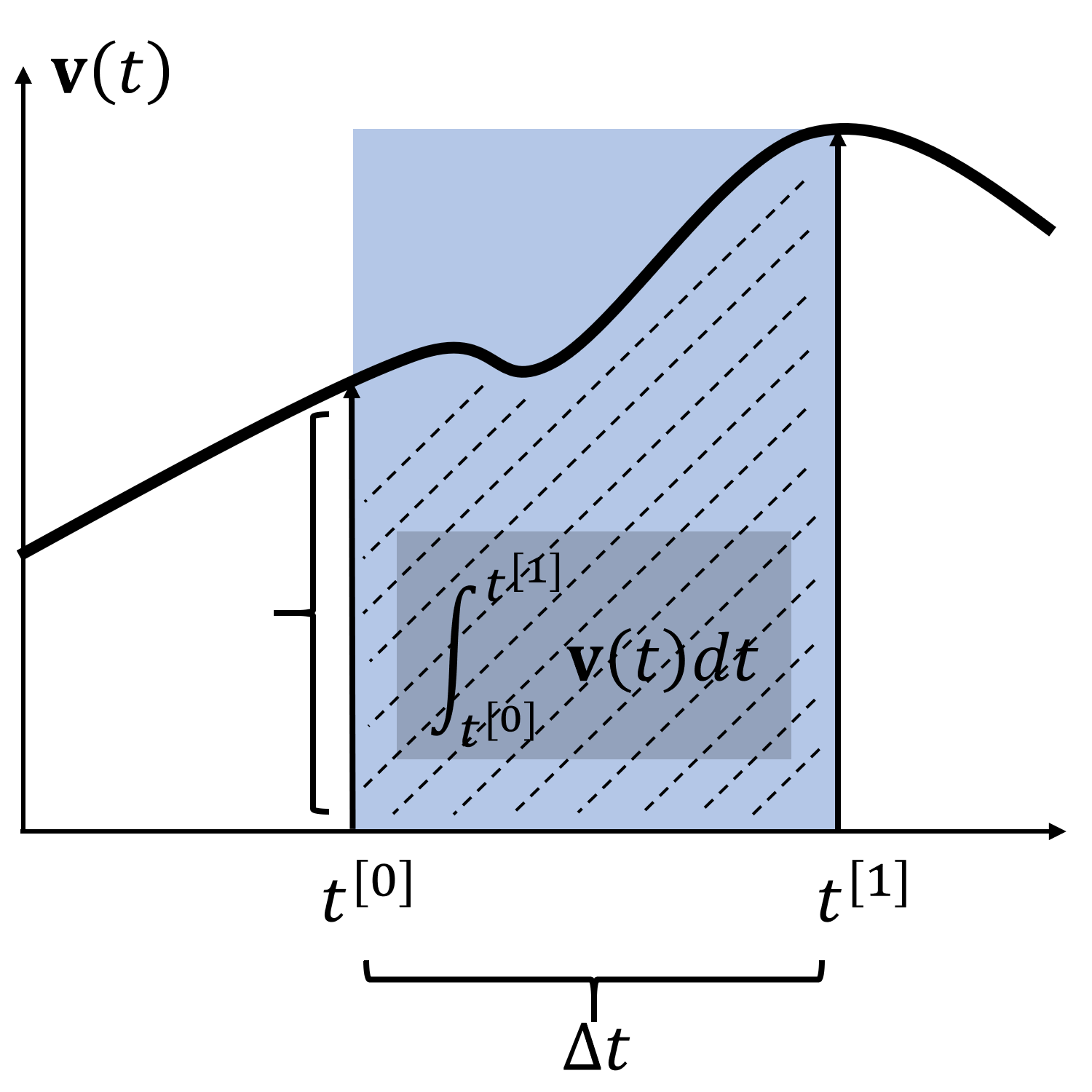
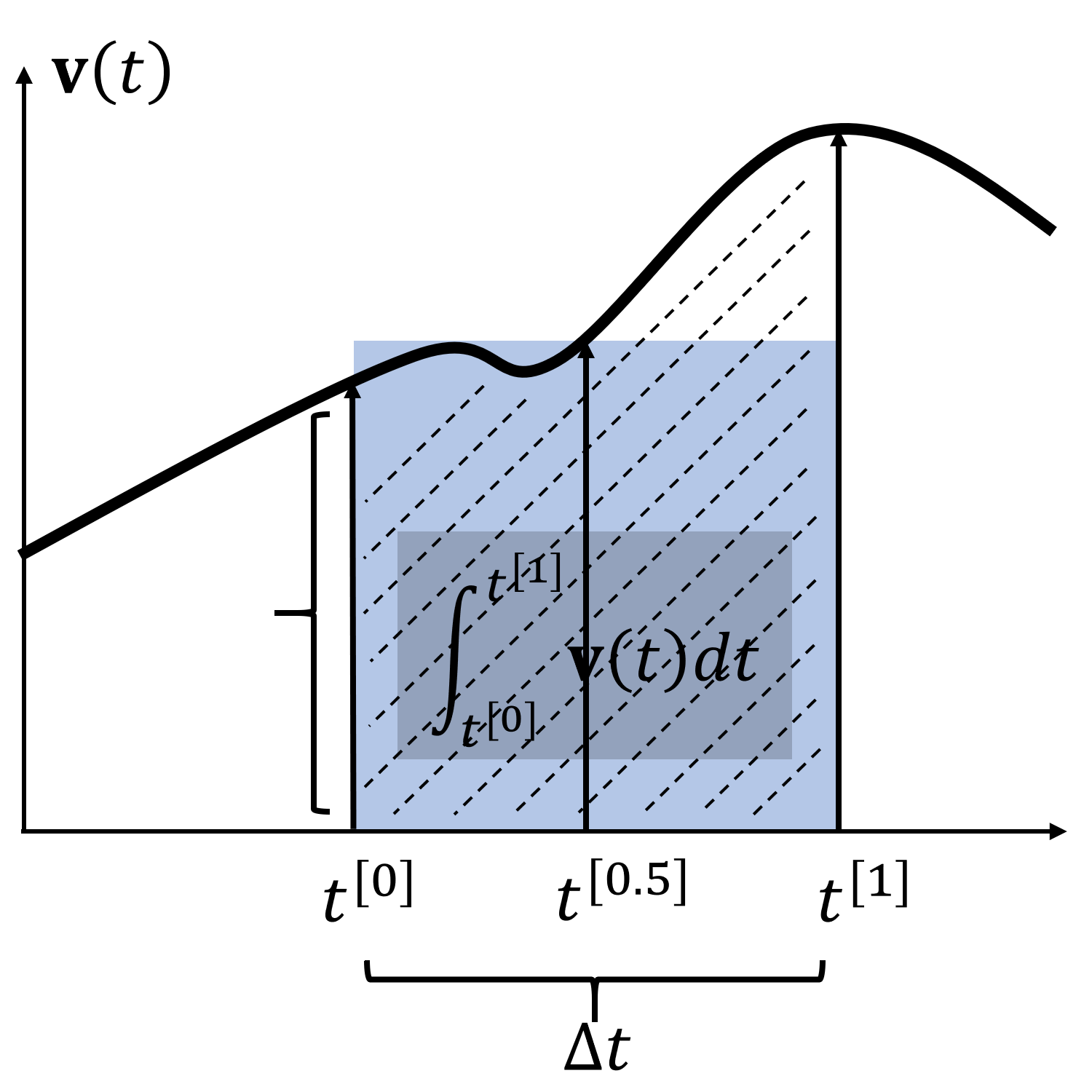
我们用上图这样的近似积分方式,就能够表达粒子随着时间的运动。那么知道了如何描述一个粒子的运动,我们就能够描述一堆粒子的运动了——换言之,我们可以开始了解一个基本的粒子系统。
基本粒子系统
我们来了解一个基本的粒子系统。在一个基本粒子系统的模拟过程中,通常包含了生成、模拟、消失三个过程,再加上把模拟过程渲染出来的渲染环节,我们分别讲解。
粒子生成
粒子生成器
粒子生成字面含义就是粒子是怎样初始化的,怎样给大量的粒子赋予初始的参数。因此我们设计了“生成器”,或者也可以称为“发射器”。
从发射器的形状说起,我们一般有点发射、平面发射、三维表面发射三种。
- 点发射顾名思义就是从同一个位置发射所有粒子,方向上有朝单一矢量、全方向两种。
- 平面发射中,平面主要有圆盘平面和多边形(三角形)平面两种。
- 三维表面发射中,以模型表面为发射器,可以认为是多个多边形平面发射的组合;另一种是在体积内发射,即在一个区域内随即发射。
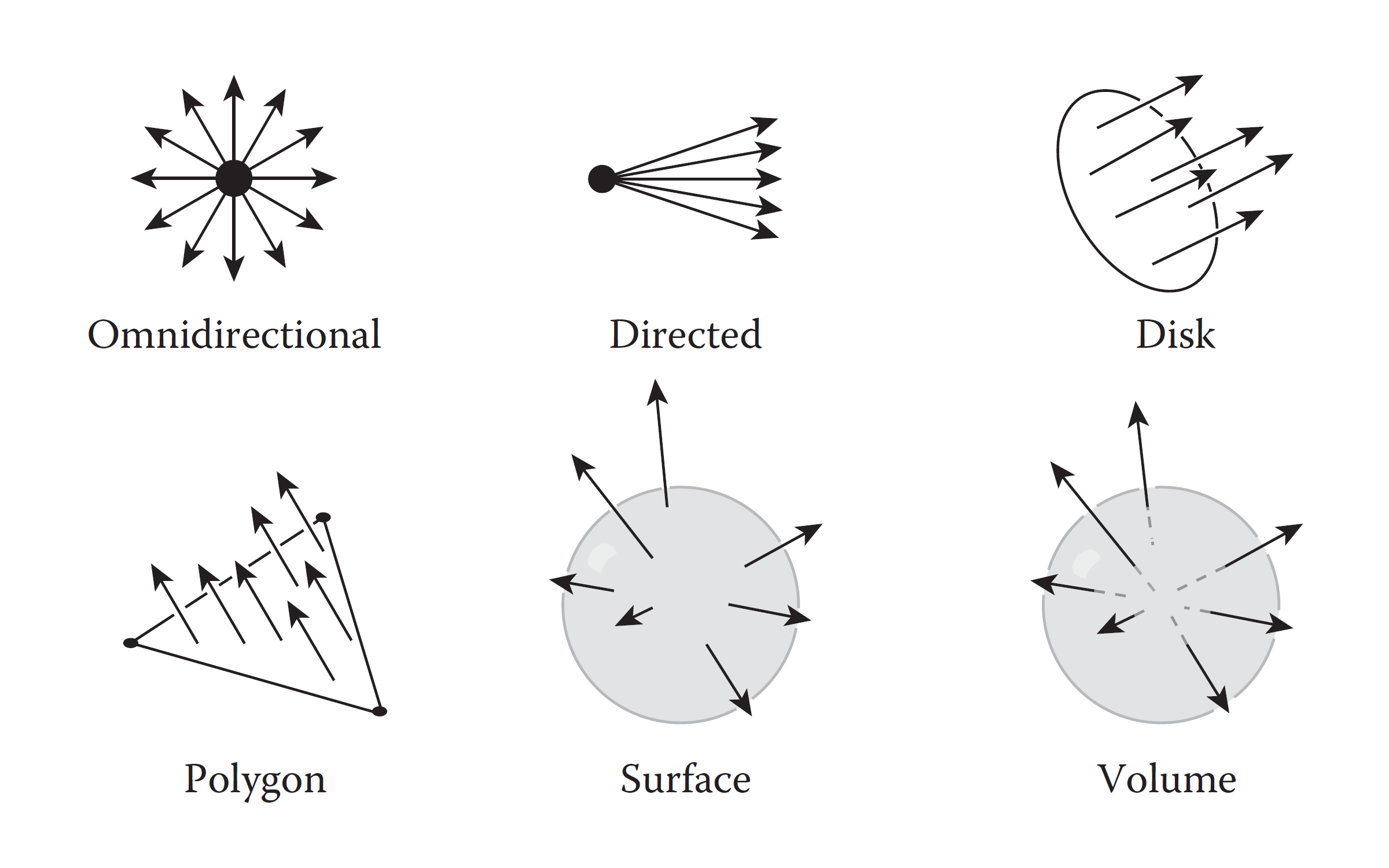
粒子生成的随机算法
我们想象,以相同的质量、速度、加速度、方向、位置等参数来初始化大量粒子会出现什么现象:所有粒子会以相同或平行的轨迹运动。所以我们这里需要使用随机算法来初始化粒子的参数、方向矢量、位置,也就是需要生成随机数、随机矢量和随机点三种数据类型。
随机数 —— 为了控制粒子形态,我们一般不会直接使用系统的 rand() 来产生均匀分布的随机数,这就涉及到随机分布的概念:
均匀分布:均匀分布即每一个数出现的概率是均等的,经典案例就是抛硬币。只有我们希望空间中充满随机的点运动时才会使用。
高斯分布 / 正态分布:概率密度函数 \(p(x)=\dfrac{1}{\sigma\sqrt{2\pi}}e^{\frac{(x-\mu)^2}{2\sigma^2}}\) (概率密度函数 PDF 指的是概率密度 - 数值,概率密度大家可以类比中学统计中的概率/区间宽度,区间宽度 -> 0) 利用高斯分布,我们就可以得到一个“大部分粒子以这个参数运动,少量随机发散”的结果,比如火花飞溅时,大部分火花都会溅射在一个区域范围内,有少量迸发到外面的样子。能够让我们更好地控制粒子的运动。
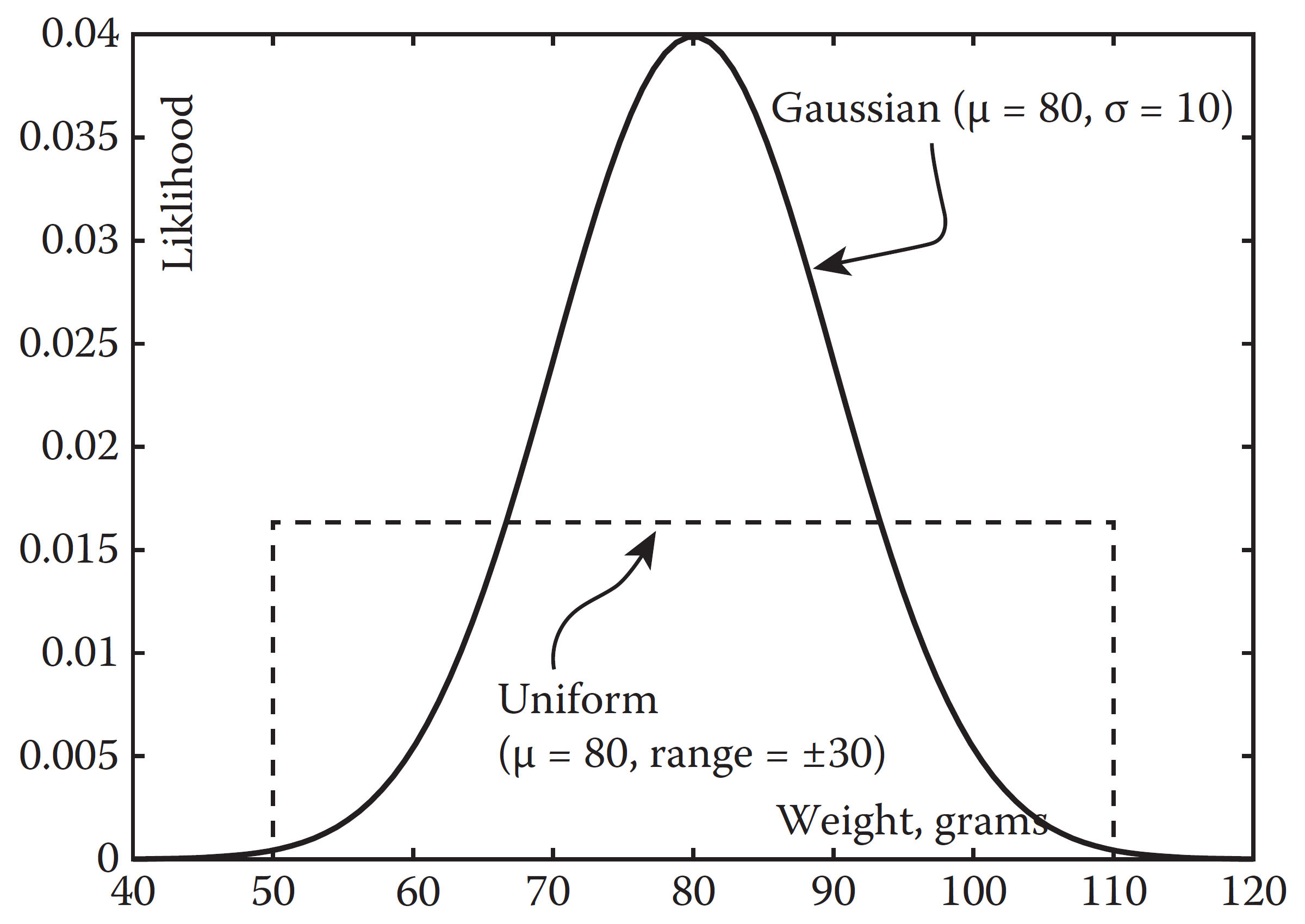
随机矢量:首先我们要了解如何生成一个均匀的球面分布,大家想象我们的地球上的任意一个点,做与球心的连线投影到赤道平面上得到长度 \(r\) ,与子午分割线成 \(\theta\) 角,那么我们只要随机 \(h=\sqrt{1-r^2}\) 和 \(\theta\) 两个值就能够得到随机矢量 \(\begin{bmatrix}r\cos\theta\\h\\r\sin\theta\end{bmatrix}\) ,经数学证明,球面上的点随 \(\theta\) 和 \(h\) 线性分布,因此,只要控制这两个随机数就可以控制球面的随机矢量。
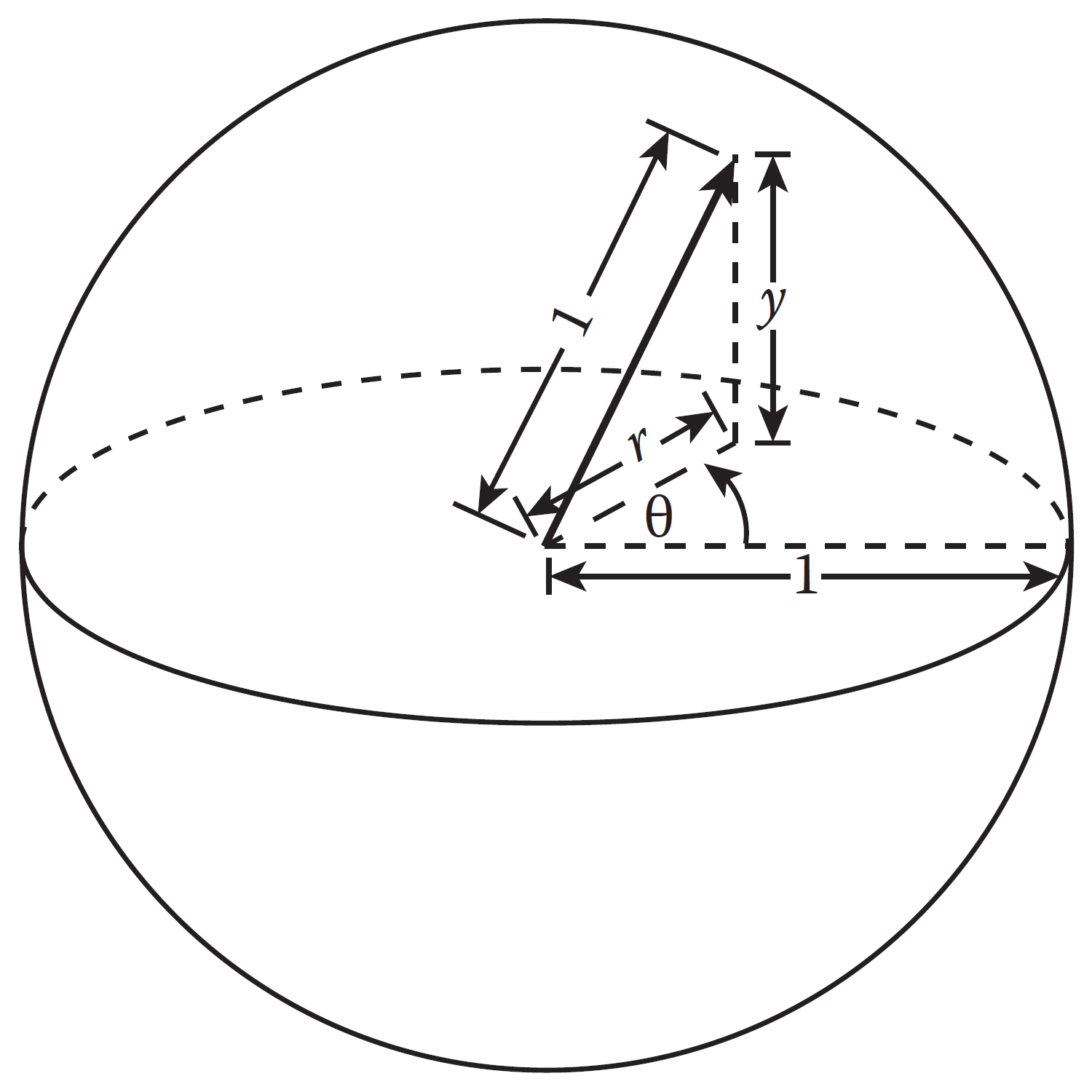
同理我们可以得到控制下图两种:点向圆盘方向发射、圆盘发射时控制随机矢量的参数,分别是\(\theta \ \phi\) 和 \(\theta\ r\) 。也就是把随机向量转换成了两个随机数的问题。
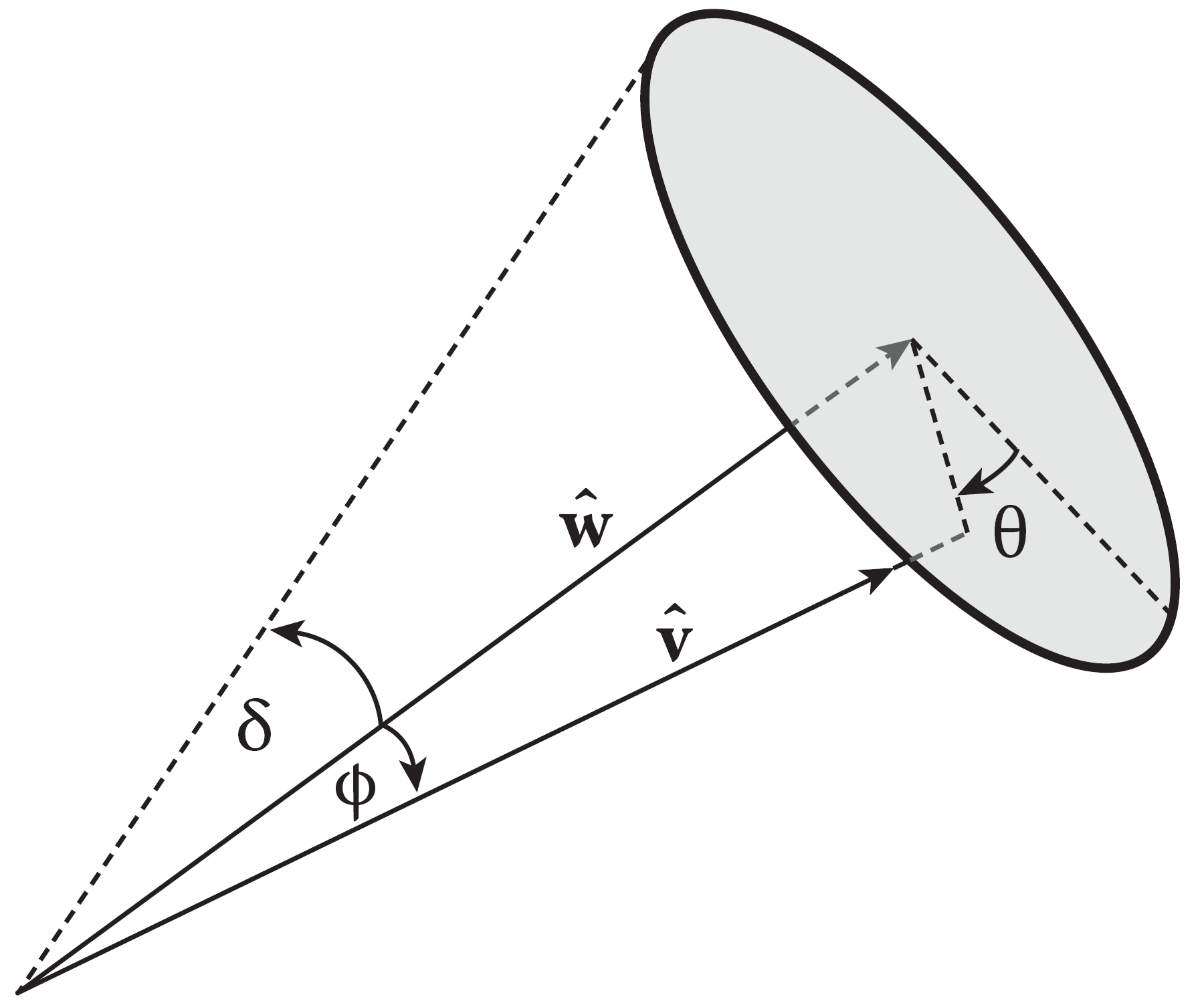
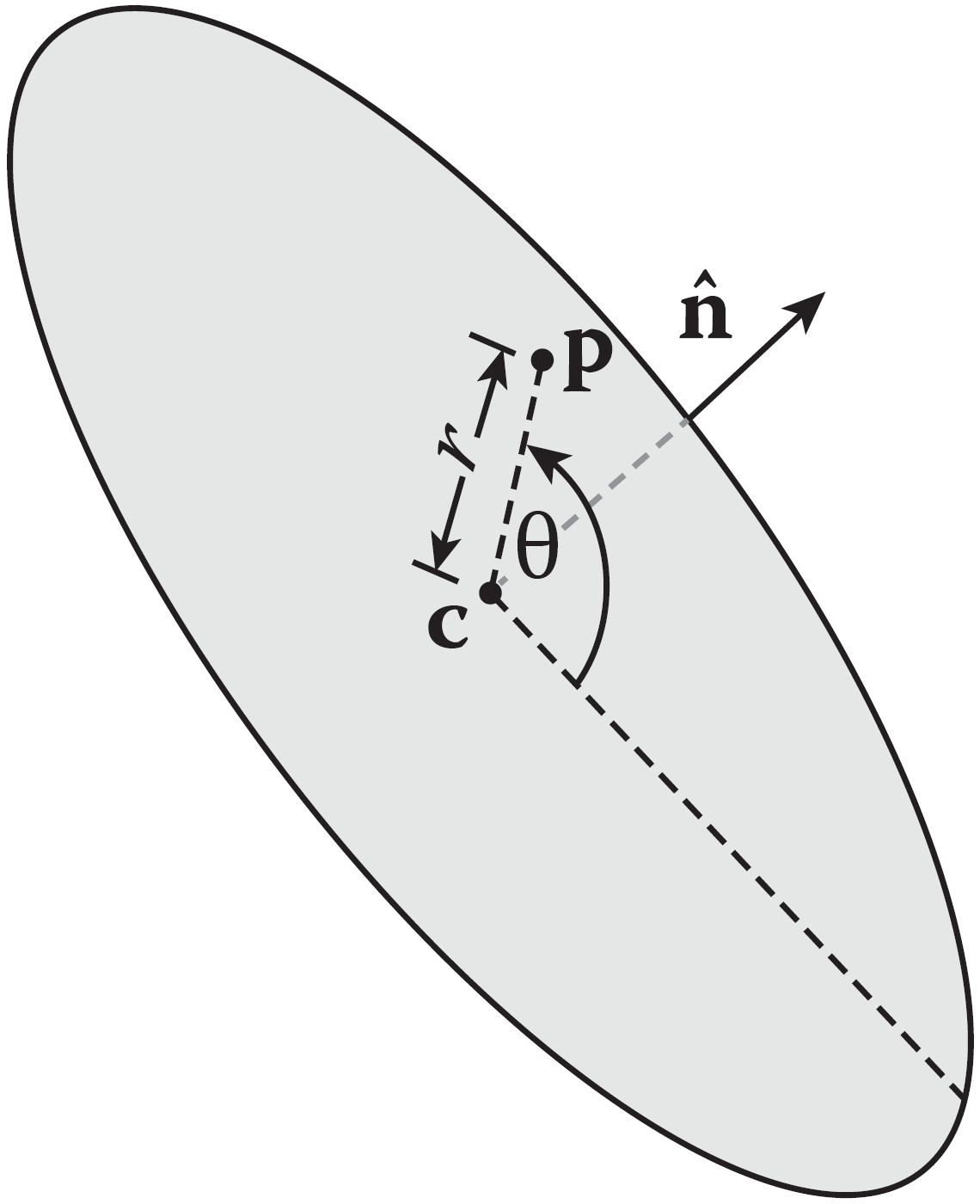
随机点:三维空间中的一个点其实就是三个数,我们按照需要来生成三个随机数即可。当然也可以用一个随机矢量(两个随机数)+随机长度(一个随机数)的方式生成。随机点主要应用于表面发射的偏移和体积内发射。
粒子模拟
碰撞
在不考虑交互的情况下(后面会专门讨论),粒子在模拟过程中除了随着力场一步一步地迭代和人工控制之外的会产生剧变的现象就是碰撞了。粒子系统通常工作在含有模型的场景中,我们就需要考虑与模型的碰撞,其实也就是与一个个平面三角形的碰撞。问题在于,粒子是一个无体积的点,而粒子所处的位置又是离散的点,粒子恰好停在一个表面的概率微乎其微,那么我们如何判定碰撞而不是让粒子直接穿越表面呢?下面我们就会讲到。
碰撞主要分为两个步骤,分别是碰撞检测和碰撞响应。首先我们得发现产生了碰撞,在发现碰撞之后,就可以执行相应的碰撞响应,这里的响应可以是让粒子消失、吸附、飞出去各种,下面举例说最简单的反弹这种。
处理一个点与一个面的碰撞主要有Penalty(惩罚)和Impulse(冲击)两种思路:
Penalty 碰撞检测:通过点与面的距离 \(\phi(x)\) 判断 碰撞响应:更新 \(f\) ,判定碰撞后的下一个时间步更新粒子状态
- Quadratic Penalty Method 碰撞条件 \(\phi(x)<0\) ,状态更新 \(f\leftarrow -k\phi(\mathbf x)\mathbf N\quad (\mathbf N为法线方向单位向量)\) 这种方法仅当粒子在面内时才能完成碰撞检测,就会出现粒子穿越表面的问题。
- Quadratic Penalty Method with a Buffer 碰撞条件 \(\phi(x)<\epsilon\) ,状态更新 \(f\leftarrow k(\epsilon-\phi(\mathbf x))\mathbf N\) 虽然缓解了粒子穿越表面的问题,但很可能会出现由于 \(k\) 过大带来的 Overshooting 现象,导致碰撞响应时,粒子就飞出去了。
- Log-Barrier Penalty Method 假定 \(\phi(x)\ge0\) 恒成立,碰撞条件 \(\phi(x)<\epsilon\) ,状态更新 \(f\leftarrow \dfrac{\rho}{\phi(\mathbf x)}\mathbf N\) 相当于在Quadratic Penalty Method with a Buffer的基础上,使Buffer的区域是可变的,一定程度上优化了上面提到的问题,但并不能根治。
Impulse 碰撞检测:通过点与面的距离 \(\phi(x)\) 判断 碰撞响应:立即更新 \(\mathbf x\) 和 \(\mathbf v\) (相当于在下一个时间步前增加一个时间步)并重新得到 \(f\) ,判定碰撞后的“下一个时间步”直接使用已经更新完的粒子状态计算。
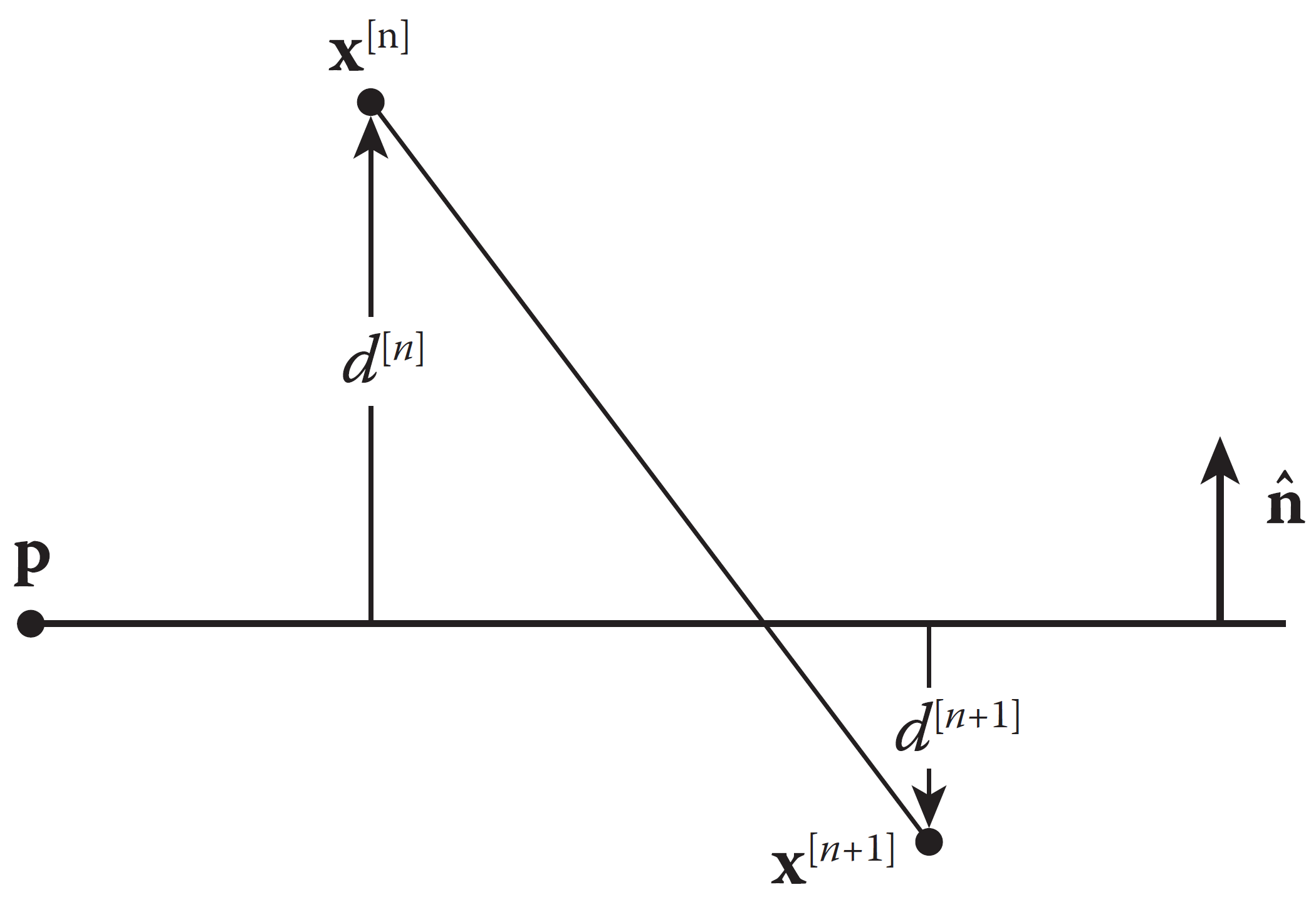
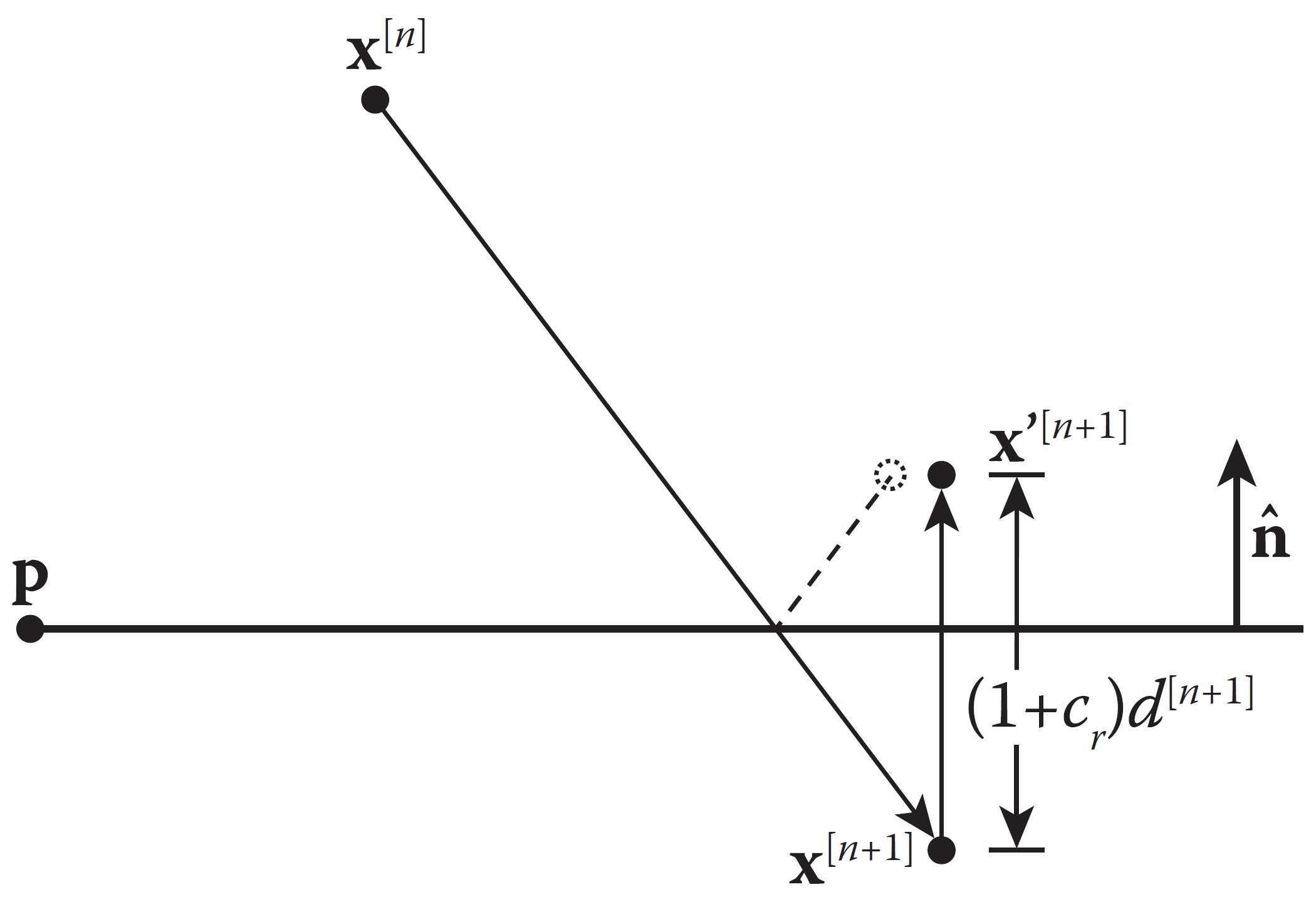
另一种理解方式是: 我们以无碰撞系统考虑两步,也就是粒子的当前位置和下一个位置,如果这两个位置分别在某个表面的两侧,那么在这个两个时间步之间一定会产生碰撞。 如下图计算,直接将下一个时间步的位置改为反弹后的位置,速度、加速度垂直于表面的分量做相应的反向即可。
粒子编排
在前面的介绍中,我们介绍了粒子的初始化和自动运行过程中的迭代、碰撞,下面我们具体来介绍我们怎样通过加速度操作和速度操作[2]来控制粒子的运动过程。
加速度操作:加速度的改变即力的改变,也即通过力场来操作粒子。例如最典型的引力,构建一个趋向于某一点的力场,粒子可能会被吸引,可能会绕它旋转,这都取决于初始速度和合力的改变,这要求我们能够熟练应用力学才能够非常熟练地操作粒子。
当然我们也可以构造一些“奇怪的力场”,比如对不同的粒子随机施加不同的加速度、为强行限制粒子的速度调整加速度、给粒子赋予一些自驱动力达到一些特殊效果(比如烟雾活起来了)之类。
速度操作:速度操作则是更加违背物理学的操作,但在视觉创作时,我们当然可以这么干——创造一些不存在的物理规律达到想要的效果。当然,通常我们不会直接将点的速度突变为一个其他值,而是不只用加速度这一个加法维度来描述速度的改变,而是用仿射变换去实现速度的变化。从而就可以得到许多奇特的效果,比如《变形金刚4》中粒子变形法的惊破天——也即让粒子塑造成一些具体的形象。
粒子渲染
这应该是我们这次课程唯一一次提到渲染——大家对三维模型的渲染都非常熟悉,体积渲染今天我们不会讲,但应该也比较容易理解。但没有体积的粒子怎样渲染呢?
- 一个经典的想法是用球体渲染,把每一个粒子当作一颗球体。但是这样不好,为什么不好,这里告诉大家如果要得到一个看起来像球体的球,我们至少需要96个面。我们知道粒子系统通常是极大规模的,再乘以一百倍,这个渲染量显然是不可接受的。
- 那么我们考虑直接以点投影到屏幕上呢。一个问题是无法看出来深度感了——深度感的来源:近大远小、近亮远暗。那么我们就可以根据深度,渲染不同半径的圆(称为面元渲染);此外还可以渲染不同的透明度。从而实现三维的感觉。但是仍然存在问题:帧率不够高时没有动态模糊,看起来就会非常卡,要知道我们大部分电影只有24帧。
- 因此,还有一种思路是“点即划痕”,也就是不渲染点,而是渲染粒子的两次时间步迭代之间的两个位置之间的连线——渲染线段,这样就自然而然带来了动态模糊。
- 粒子不只能表述一个点,还可以用于表述以点方式运动的物体。那么这个物体我们可以在渲染时表现出来。第一种是用材质,每一个粒子渲染一个矩形(也就是两个三角形),在矩形上上一个材质。这种渲染我们称之为“精灵”。
- 当然,“精灵”的渲染方式只能将粒子替换成平面,有时候我们还是需要用三维的东西去表现旋转等运动,比如落叶。所以我们也可以用几何形体去替换粒子,最后渲染模型。
- 最后一种思维是体积渲染,一般用于极大规模的粒子系统,比如流体、核爆。极大规模的渲染中对粒子逐个渲染显然不现实,我们把粒子所处的区域体素化,再渲染体积,也可以在体积上去处理材质。
案例分析与欣赏
Pyro烟雾案例(自制)
粒子影片案例
交互粒子系统
前面我们介绍了没有交互的基本粒子系统,现在我们进一步提高一下复杂度,给粒子之间加上交互。粒子之间的交互换句话说就是:每一个粒子都对其他每一个粒子施加了力,也就是每一次迭代,对每一个粒子都要做 \(n-1\) 次力的叠加。复杂度上相较无交互的粒子系统 \(O(N)\) 大幅提高至 \(O(N^2)\) ,计算量急剧增加。
foreach particle i do
Calculate the resultant force F on i;
foreach particle j do
Calculate the sum of the forces j acting on i
end
end
foreach particle j do
Update status of i
end减少计算量的可能性
这种复杂度是无法通过计算方法的优化来减少复杂度:每一个数据读取一遍就是 \(O(N^2)\) 了。因此我们只能考虑减少参与计算的数据。我们考虑到在真实物理世界中,粒子间的效应(即力)随着物理距离的增加急剧变弱——也就是我们常见的平方反比定律,引力场、电磁场均满足这条定律。因此我们可以忽略距离粒子足够远的粒子,或者是将远处的外围粒子做一簇一簇的近似计算而非精确计算。要完成这样的优化方法,我们首先得把粒子组成一簇一簇的,组合方法这里介绍均匀空间网格、八叉树、kd树三种。
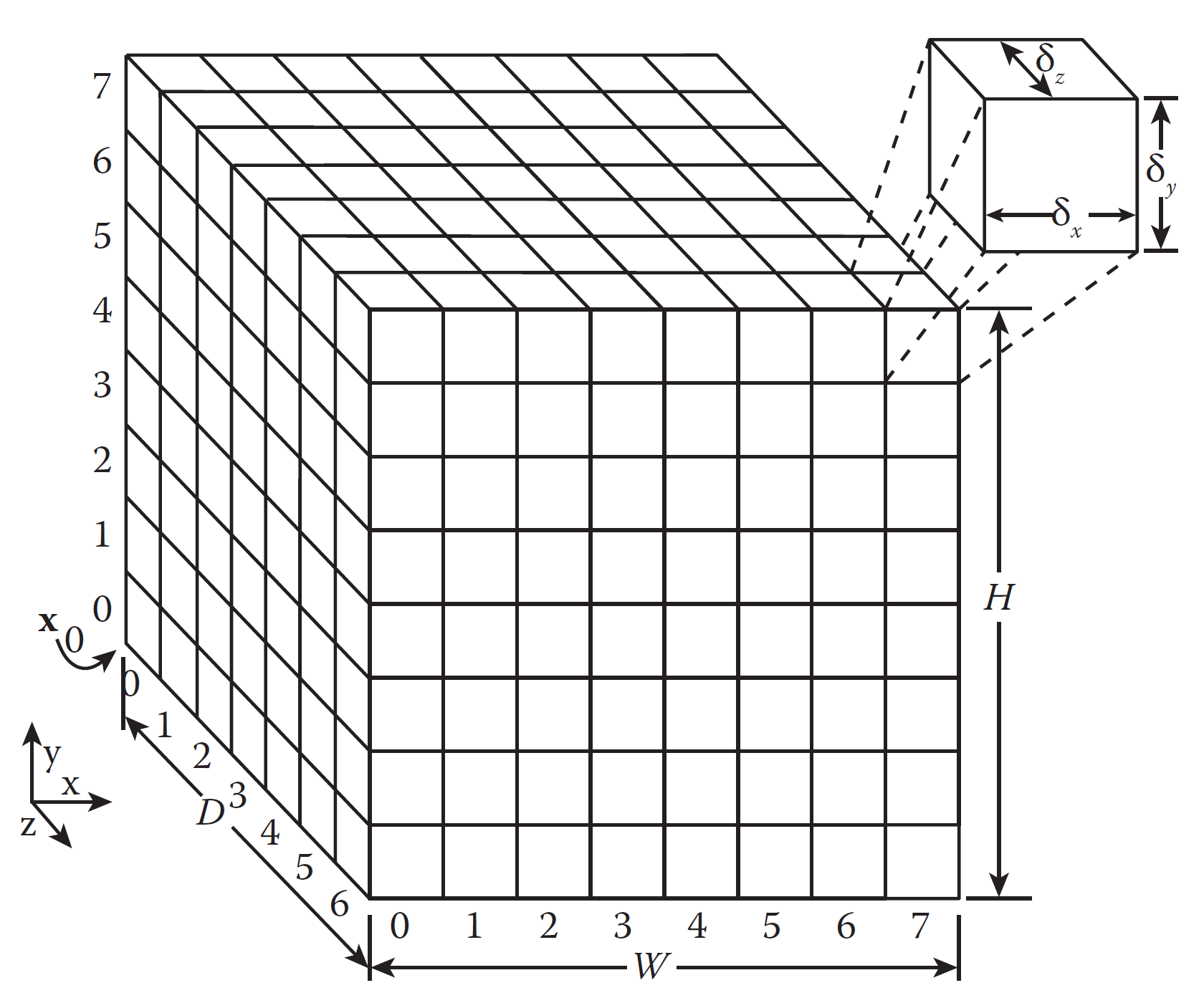
- 均匀空间网格:最为简单的组合方法,将空间按一定的长方体网格分割,来组合粒子。这样网格利用率很低。
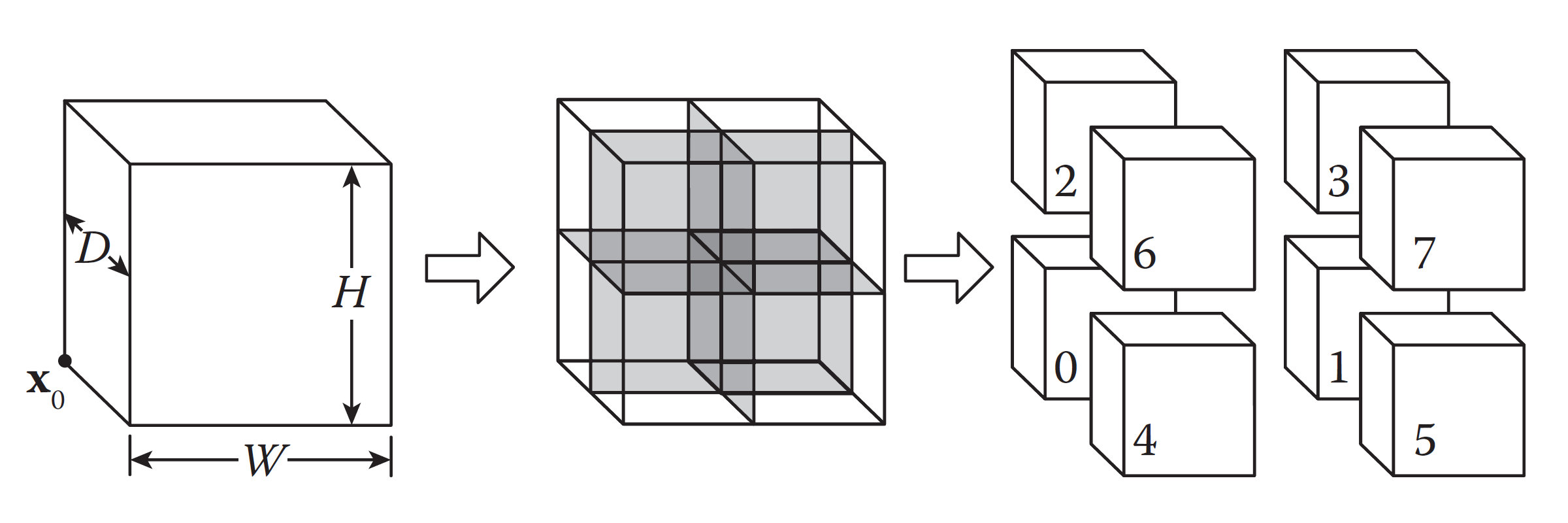
- 八叉树:八叉树则是经典的一分八方法,就如我们能把一个矩形同样宽高比地分成四份一样,把一个长方体分割成八份,从而建立树结构。这样我们可以根据粒子的不均匀排布来分割空间。
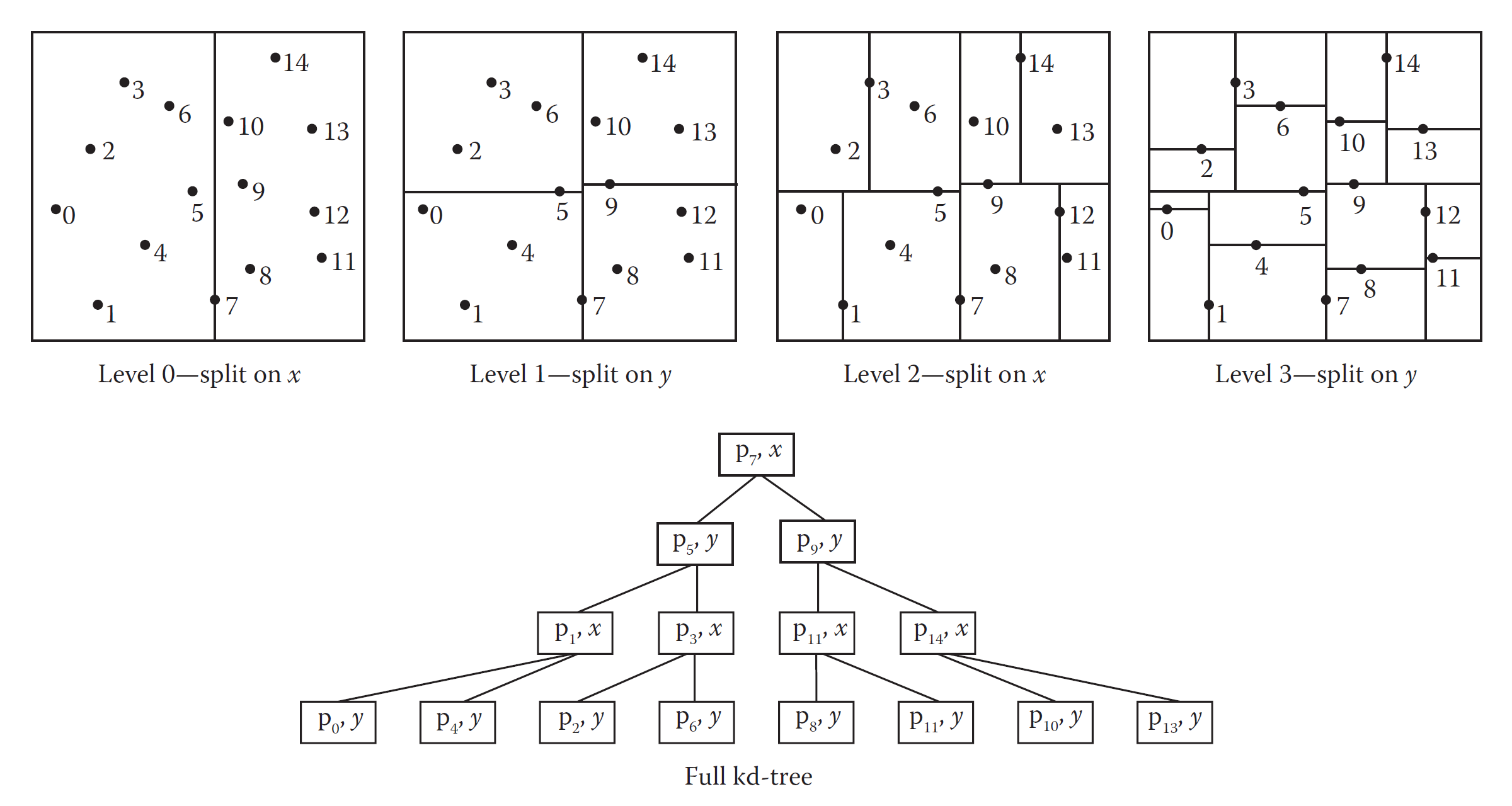
- kd树:kd树则是一种二叉树,也是渲染领域光线追踪算法中BVH的构建基础。我们生成一个能够恰好包含所有粒子的包围盒,再以其中某一个维度上所有点的中位值分割。这种分割方法的每个单元粒子数量相近,范围搜索非常方便。利用kd树忽略或近似部分计算,可以减少计算复杂到 \(O(N\log N)\) 。
以天文系统、群集系统为例的交互粒子系统
天文系统
天文系统是最典型的简单交互粒子系统:天体的大小相比较之间的距离可以抽象化为质点;粒子之间存在相互引力——且只有相互引力。天体 \(i\) 收到天体 \(j\) 的引力为 \(F_i^j = G\dfrac{m_im_j}{r_{ij}^2}\hat\mathbf x_{ij}\) 。
而天文系统中,天体之间的质量差距、两个星系之间的距离都非常之大——大到可以忽略掉很大部分的力。比如地球受到最近的恒星系比邻星的引力已经微乎其微,就算需要精确计算,也只需要将比邻星系作为一个整体来考虑。
因此,天文系统非常适合实践我们前面提到的空间优化方法,我们将这种远距离的粒子聚成的整体称为“聚簇”,我们可以很快地估算一个聚簇带来的引力。根据天体系统的特征,我们还可以用不同大小的簇:例如仙女星系对太阳的引力,和一个相邻星系的引力,各自用一个簇来计算是合理的,这两个簇的大小显然不一样。
群集系统
另一个例子是:给粒子赋予生命,或者说赋予一些“意识力”。这个力显然不是一个物理力学上的力,而是我们用粒子系统来模拟大规模生物的运动,例如鸟群。模拟生命体的运动,就会有更加复杂的逻辑表达。
[3]我们将群集系统中的一个被模拟生命体称为“boid”,假定每个boid遵循三个规则:碰撞规避、速度匹配、集中,根据这三个规则得到三个加速度,根据三个加速度的有权或无权加和作为迭代用的加速度。
- 碰撞规避:越靠近另一个“boid”,反向飞离的速度就越大 \(a_{ij}^a=-\dfrac{k_a}{d_{ij}}\hat{x}_{ij}\)
- 速度匹配:与“同伴”保持相对速度,保持群体运动一致性 \(a_{ij}^v=k_v(\mathbf v_j-\mathbf v_i)\)
- 集中:朝向近邻的加速度,以保持群体完整 \(a_{ij}^c=k_c\mathbf x_{ij}\)
距离与视域:现在我们要考虑需要计算哪些 \(boid_j\) 。考虑真实生物,就会发现距离远的看不到、视线外的看不到。按照这两条,我们可以分别得到两个关于距离和视域的近邻boid的计算权重,以加权值来作为最终迭代使用的加速度。
加速度的权重:根据不同生物、环境的特点,三种加速度的“紧迫程度”不一样,而生物能达到的加速度是有限的。那么可以根据具体情况,分配三种加速度最终加权计算的权重。
外界干扰:绕过障碍:如果没有外界干扰,上述条件就能使我们的群集系统运作起来了。但环境中往往出现障碍——在“有生命”的群集中,不太可能傻乎乎地直接就碰撞了。所以我们可以为环境中的障碍物建立带有斥力的势场、操控粒子根据“观察角度”中出现的障碍更新加速度等方式处理避障。
案例分析与欣赏
群集系统影片案例
交互粒子系统还可以引入黏度等更加复杂的交互力,来模拟更加复杂的系统。在流体的章节中,我们会再次见到基于交互粒子系统的流体模拟方法。
弹性网格
粒子这一节的最后,我们来讲一种基于粒子的其他模型——严格说就不再是典型的粒子系统了。我们在粒子之间添加了一根线、比如一根“弹簧”,就构成了我们的可形变弹性网格[4]。这种结构可以就可以用于我们的头发、布料、软体模拟,再比如我们在DCC软件中常用的晶格变形器:驱动刚体的扭曲变形。由于时间的关系,我们这次的课程没有单开对应的章节,只是在粒子这一章,介绍其中的一种基于粒子的方法。
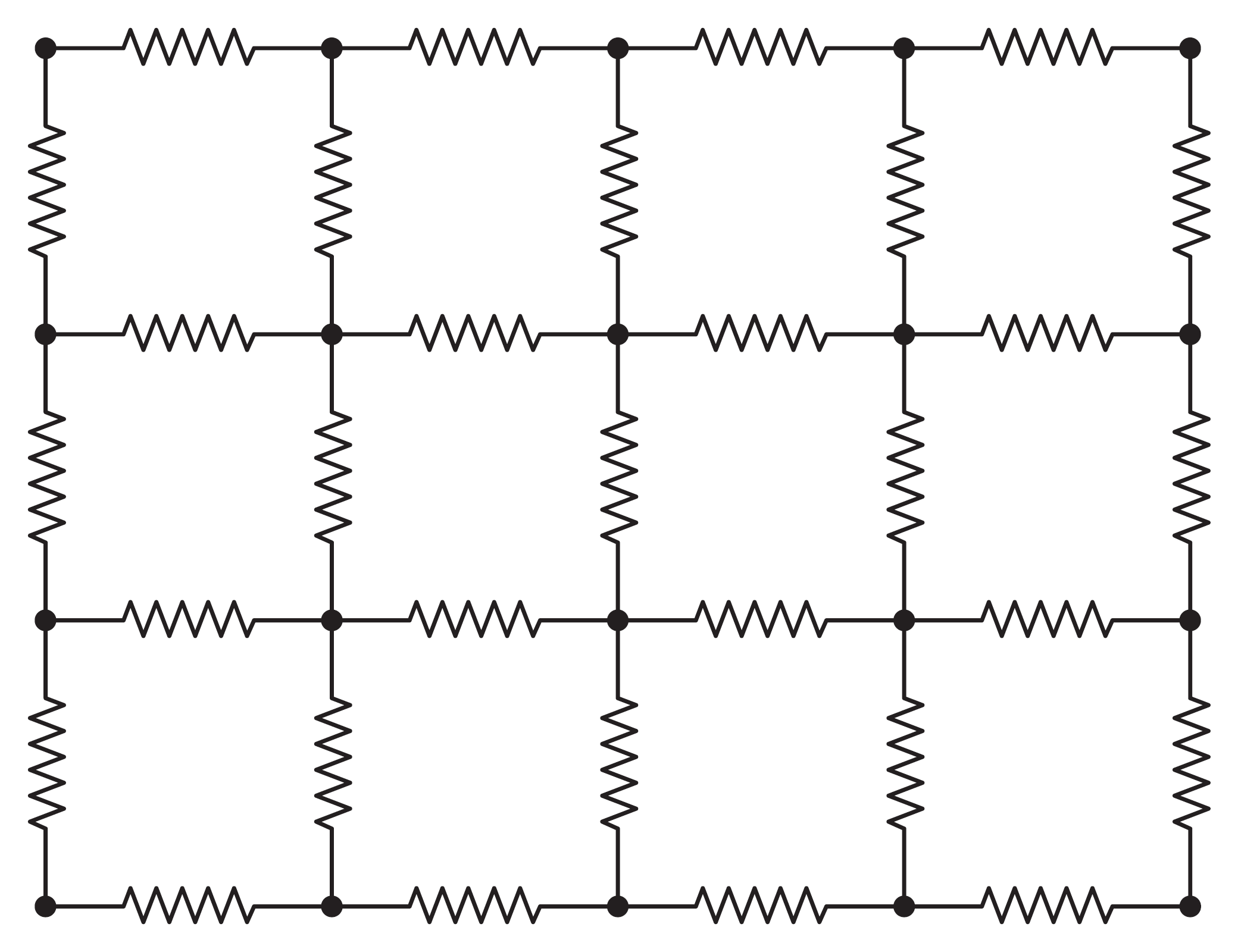
弹簧-质量-阻尼模型
弹簧-质量-阻尼模型是可形变弹性网格的核心系统,即粒子之间的连接所施加的力由弹力和阻力两种。
- 弹力: \(\mathbf f_k=-kx\) , \(k\) 为劲度系数(\(x\) 为形变长度)
- 阻力: \(\mathbf f_d=-dv\) , \(d\) 为阻尼系数(通常得到的是阻尼因子 \(\zeta=\dfrac{d}{2\sqrt{km}}\))
设其他外力和为 \(\mathbf f_e\) ,则有 \(ma=\mathbf f_e-kx-dv\) 即 \(m\ddot{x}+d\dot{x}+kx=\mathbf f_e\) ,又是一个二阶微分方程。
面的受力
当我们将点连接起来时,不可避免地就出现了面。虽然面不参与与粒子的交互,但面受到阻力、风等外部力的作用效果也需要参与到粒子的迭代计算中去。这里主要是有升力和空气阻力两种力,前者推动网格运动,后者阻碍。这里时间原因我们就不再详细分析。
- 升力: \(\mathbf f_d=-C_dA(\hat \mathbf n\dot\ \mathbf v_r)\mathbf v_r\)
- 拖拽力: \(\mathbf f_l=-C_lA(\hat \mathbf n\dot\ \mathbf v_r)(\mathbf v_r\times\dfrac{\hat \mathbf n\times\mathbf v_r}{\left \|\hat \mathbf n\times\mathbf v_r\right \| })\)
弹性网格模拟
对每一个粒子,逐连接体、逐面计算合力。
foreach particle do
Calculate F_e;
foreach rod do
Calculate F_k and F_d
foreach face do
Calculate F_face
end
end
end
foreach particle i do
Update status of i
end碰撞
这里,我们需要用一个形体的观点来看待弹性网格了,这与粒子的碰撞截然不同了。对于一个几何形体,我们需要从点、线、面三个结构上来判定碰撞。实际情况中,“顶点与顶点”、“顶点与线”、“线与面”的碰撞情况非常少——概率几乎为零,因此我们一般只会判断“顶点与面”和“边与边”。
- 顶点-面检测:这种检测我们在介绍粒子碰撞时就已经提过。
- 边-边检测:思路上是取两条线上面到另一条线最近的点(作垂面交点),求这两个点的距离。
案例分析与欣赏
布料系统影片案例
[1] Particle systems - A technique for modeling a class of fuzz objects [2] Particle animation and rendering using data parallel computation [3] Flocks, Herds, and Schools: A Distributed Behavioral Model [4] The behavioral test-bed: Obtaining complex behavior from simple rules